Equal

lhs==rhs

returns True if lhs and rhs are identical.

Details

  • lhs==rhs is used to represent a symbolic equation, to be manipulated using functions like Solve.
  • lhs==rhs returns True if lhs and rhs are ordinary identical expressions.
  • lhs==rhs returns False if lhs and rhs are determined to be unequal by comparisons between numbers or other raw data, such as strings.
  • Approximate numbers with machine precision or higher are considered equal if they differ in at most their last seven binary digits (roughly their last two decimal digits).
  • For numbers below machine precision, the required tolerance is reduced in proportion to the precision of the numbers.
  • 2==2. gives True.
  • e1==e2==e3 gives True if all the ei are equal.
  • Equal[e] gives True.
  • For exact numeric quantities, Equal internally uses numerical approximations to establish inequality. This process can be affected by the setting of the global variable $MaxExtraPrecision.
  • Equal remains unevaluated when lhs or rhs contains objects such as Indeterminate and Overflow.
  • In StandardForm and InputForm, lhs==rhs can be input as lhs\[Equal]rhs or lhsrhs.
  • It can also be input as \[LongEqual] or lhsrhs.
  • In TraditionalForm, lhs==rhs is output as lhsrhs.

Background & Context

  • Equal[expr1,expr2] returns True if expr1 and expr2 are numerically equal, False if they are unequal and unevaluated if equality cannot be established. For example, Equal[(1+Sqrt[5])/2,GoldenRatio] returns True, Equal[1,2] returns False and Equal[1,a] returns unevaluated. Equal[expr1,expr2] may be input using double equal signs as expr1==expr2 or using the \[Equal] character as expr1expr2. The multiple-argument form Equal[expr1,expr2,…], which may also be input as expr1==expr2…, returns True if all expressions expri are numerically equal, False if at least two are not equal and unevaluated otherwise. The single-argument form Equal[expr] returns True (as, slightly paradoxically, does the single-argument form Unequal[expr]).
  • Numbers with machine precision (MachinePrecision) or greater are considered equal if they differ in at most their last seven binary digits. Equality for numbers below machine precision is established based on agreement to within the precision of the lowest precision number. For example, 1.01`2==1 returns True, while 1.01`3==1 returns False. For exact numeric quantities, Equal uses numerical approximations to establish inequality, which can be affected by the value of the global variable $MaxExtraPrecision.
  • Equal is related to a number of other symbols. Set[expr1,expr2] (which may be input using the "single equals" syntax expr1=expr2) evaluates expr2 and assigns the result to be the value of expr1, while SameQ[expr1,expr2] (which may be input using the "triple equals" syntax expr1===expr2) returns True if expr1 and expr2 are identical and otherwise returns False. In contrast to Equal, SameQ differentiates between different representations of numbers; for example, SameQ[1,1.] and SameQ[1.,1.+0.I] both return False. The behavior of SameQ also differs from that of Equal in that SameQ always evaluates to True or False, whereas Equal may remain unevaluated in cases where equality cannot be resolved. Unequal (which may be input as expr1!=expr2 is the converse of Equal. Equal also has an operator form EqualTo. The Boolean logic analog of Equal is Equivalent.
  • PossibleZeroQ can be used to indicate if a given expression has value 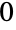in some cases where Equal returns unevaluated. For example, Equal[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0] returns evaluated, while calling PossibleZeroQ on its first argument returns True (together with an informative message indicating that a zero value could not be rigorously established). Symbolic simplifiers like Simplify, FullSimplify and RootReduce can sometimes also be used to rigorously establish equality (including in the example just given) when Equal cannot.

Examples

open allclose all

Basic Examples  (2)

Test equality:

Represent an equation:

Scope  (12)

Numeric Equalities  (6)

Test equality of numbers:

Approximate numbers that differ in their last seven binary digits are considered equal:

Compare an exact numeric expression and an approximate number:

Compare two exact numeric expressions; a numeric test may suffice to disprove equality:

Proving equality requires symbolic methods:

Symbolic methods used by Equal are insufficient to prove this equality:

Use RootReduce to decide whether two algebraic numbers are equal:

Numeric methods used by Equal do not use sufficient precision to disprove this equality:

RootReduce proves that the two algebraic numbers are not equal:

Increasing $MaxExtraPrecision may also allow you to disprove equality:

Symbolic Equalities  (6)

A symbolic identity:

Equal does not automatically prove this identity:

Use Expand to prove it:

A symbolic equation:

Use Solve to solve the equation:

Reduce gives all solutions, including the ones that require nongeneric values of parameters:

Compare more than two expressions:

Compare lists:

Compare strings:

Properties & Relations  (6)

The negation of two-argument Equal is Unequal:

The negation of three-argument Equal does not simplify automatically:

Use LogicalExpand to express it in terms of two-argument Unequal:

The negation of three-argument Equal is not equivalent to three-argument Unequal:

Equal tests mathematical equality of objects represented by expressions:

SameQ tests syntactic equality of expressions:

When Equal cannot decide whether two numeric expressions are equal it returns unchanged:

FullSimplify uses exact symbolic transformations to prove the equality:

PossibleZeroQ uses numeric and symbolic heuristics to decide whether an expression is zero:

Numeric methods used by PossibleZeroQ may incorrectly decide that a number is zero:

Use Solve to solve equations for generic values of parameters:

Reduce gives all solutions, including those with nongeneric parameter values:

Use Reduce to solve equations over specified domains:

Possible Issues  (5)

Equality for machine-precision approximate numbers can be subtle:

The extra digits disrupt equality:

Arbitrary-precision approximate numbers do not have this problem:

Thanks to automatic precision tracking, Equal knows to look only at the first 10 digits:

In this case, the equality test for machine numbers succeeds:

The extra digits in this case are ignored by Equal:

Equality may not be transitive for approximate numbers:

Equal is not treated as the Boolean equivalence operator:

Use Equivalent instead:

Wolfram Research (1988), Equal, Wolfram Language function, https://reference.wolfram.com/language/ref/Equal.html (updated 2007).

Text

Wolfram Research (1988), Equal, Wolfram Language function, https://reference.wolfram.com/language/ref/Equal.html (updated 2007).

CMS

Wolfram Language. 1988. "Equal." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Equal.html.

APA

Wolfram Language. (1988). Equal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Equal.html

BibTeX

@misc{reference.wolfram_2024_equal, author="Wolfram Research", title="{Equal}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Equal.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_equal, organization={Wolfram Research}, title={Equal}, year={2007}, url={https://reference.wolfram.com/language/ref/Equal.html}, note=[Accessed: 24-November-2024 ]}