WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

Quartics
✖
Quartics

✖

代数方程式を解くことを含む関数のオプションで，四次方程式の解に陽的な形を与えるべきかどうかを指定する．

詳細

  • Quartics->Trueのとき，四次方程式の根は，累乗根の形で明示的に与えられる．Quartics->Falseのときは，際立って簡単な形を持たない三次方程式の根はRootオブジェクトを使って陰的に与えられる．
  • Quartics->Trueとすると，かなり大きい出力となることがある．

例題

すべて開くすべて閉じる

例  (1)基本的な使用例

デフォルトで，Reduceは累乗根の四次方程式を解くのに一般的な公式は用いない：

In[1]:=1
✖
https://wolfram.com/xid/0i1u2zj6s-ej107d
Out[1]=1

Quartics->Trueとすると，Reduceはすべての四次方程式を累乗根によって解く：

In[2]:=2
✖
https://wolfram.com/xid/0i1u2zj6s-jxrryz
Out[2]=2

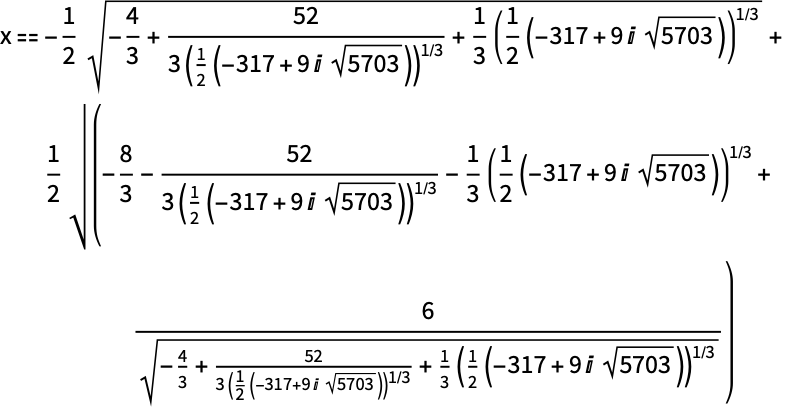
この簡単な四次方程式累乗根で解くのに一般的な公式は必要ない：

In[3]:=3
✖
https://wolfram.com/xid/0i1u2zj6s-ei3pte
Out[3]=3

スコープ  (2)標準的な使用例のスコープの概要

デフォルトで，Eigenvaluesは累乗根の四次方程式を解くのに一般的な公式は使わない：

In[1]:=1
✖
https://wolfram.com/xid/0i1u2zj6s-c8akaq
Out[1]=1

Quartics->Trueとすると，すべての四次方程式が累乗根によって解かれる：

In[2]:=2
✖
https://wolfram.com/xid/0i1u2zj6s-k2ahxd
Out[2]=2

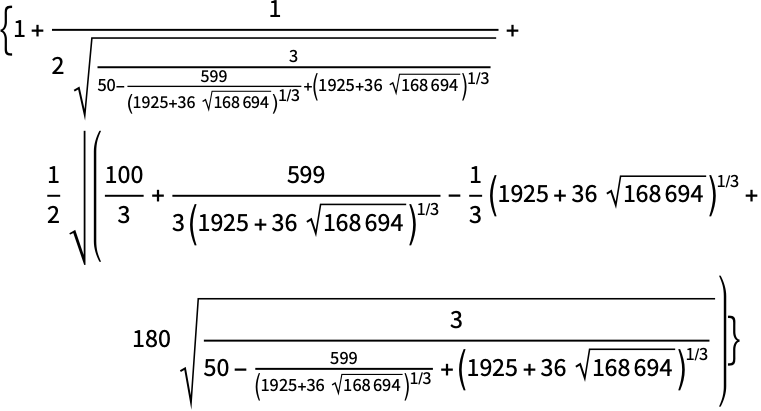
デフォルトで，ToRadicalsはすべての四次Rootオブジェクトを累乗根に変換する：

In[1]:=1
✖
https://wolfram.com/xid/0i1u2zj6s-frjrx0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1u2zj6s-f9wzrt
Out[2]=2

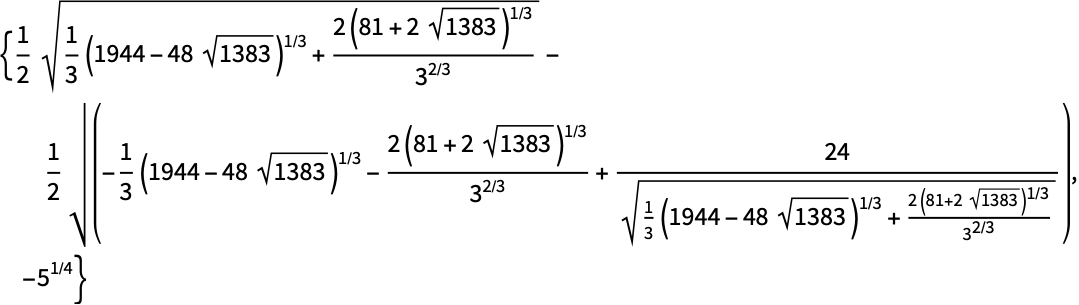
Quartics->Falseとすると，ToRadicalsは四次方程式を解くのに一般的な公式は使わない：

In[3]:=3
✖
https://wolfram.com/xid/0i1u2zj6s-d95fye
Out[3]=3
Wolfram Research (1988), Quartics, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartics.html.
✖
Wolfram Research (1988), Quartics, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartics.html.

テキスト

Wolfram Research (1988), Quartics, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartics.html.

✖
Wolfram Research (1988), Quartics, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartics.html.

CMS

Wolfram Language. 1988. "Quartics." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Quartics.html.

✖
Wolfram Language. 1988. "Quartics." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Quartics.html.

APA

Wolfram Language. (1988). Quartics. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quartics.html

✖
Wolfram Language. (1988). Quartics. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quartics.html

BibTeX

@misc{reference.wolfram_2025_quartics, author="Wolfram Research", title="{Quartics}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Quartics.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_quartics, author="Wolfram Research", title="{Quartics}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Quartics.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_quartics, organization={Wolfram Research}, title={Quartics}, year={1988}, url={https://reference.wolfram.com/language/ref/Quartics.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_quartics, organization={Wolfram Research}, title={Quartics}, year={1988}, url={https://reference.wolfram.com/language/ref/Quartics.html}, note=[Accessed: 04-April-2025 ]}