RamanujanTau[n]
gives the Ramanujan ![]() function
function ![]() .
.


RamanujanTau
RamanujanTau[n]
gives the Ramanujan ![]() function
function ![]() .
.
Details
- Integer mathematical function.
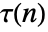 gives the coefficient of
gives the coefficient of 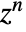 in the series expansion of
in the series expansion of 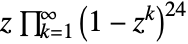 .
.- RamanujanTau automatically threads over lists.
Examples
open all close allBasic Examples (2)
Scope (12)
Numerical Evaluation (3)
Evaluate efficiently for large values of the argument:
Compute the elementwise values of an array:
Or compute the matrix RamanujanTau function using MatrixFunction:
Visualization (3)
Plot the RamanujanTau function:
Plot the contours of the RamanujanTau function:
Plot the RamanujanTau function in three dimensions:
Function Properties (4)
RamanujanTau is only defined for integer inputs:
RamanujanTau threads over lists:
RamanujanTauL is everywhere singular:
Applications (7)
Logarithmic plot of RamanujanTau:
The first prime value of RamanujanTau:
The first 20,000 values are nonzero, satisfying Lehmer's conjecture [more info]:
Relation with DedekindEta:
The summatory ![]() -function [more info]:
-function [more info]:
Relation with DedekindEta:
Properties & Relations (7)
The first 10 values of RamanujanTau using Product:
RamanujanTau is multiplicative for coprime integers:
Representation of an integer as the sum of 24 squares:
RamanujanTauL is the Dirichlet ![]() -function associated with RamanujanTau:
-function associated with RamanujanTau:
FindSequenceFunction can recognize the RamanujanTau sequence:
Neat Examples (3)
Successive differences of RamanujanTau modulo 3:
A representation of zero in terms of RamanujanTau:
Tech Notes
Related Guides
History
Text
Wolfram Research (2007), RamanujanTau, Wolfram Language function, https://reference.wolfram.com/language/ref/RamanujanTau.html.
CMS
Wolfram Language. 2007. "RamanujanTau." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RamanujanTau.html.
APA
Wolfram Language. (2007). RamanujanTau. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RamanujanTau.html
BibTeX
@misc{reference.wolfram_2025_ramanujantau, author="Wolfram Research", title="{RamanujanTau}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/RamanujanTau.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_ramanujantau, organization={Wolfram Research}, title={RamanujanTau}, year={2007}, url={https://reference.wolfram.com/language/ref/RamanujanTau.html}, note=[Accessed: 09-March-2026]}