Product

Product[f,{i,i_max}]

evaluates the product .

Product[f,{i,i_min,i_max}]

starts with .

Product[f,{i,i_min,i_max,di}]

uses steps di.

Product[f,{i,{i₁,i₂,…}}]

uses successive values i₁, i₂, ….

Product[f,{i,i_min,i_max},{j,j_min,j_max},…]

evaluates the multiple product .

Product[f,i]

gives the indefinite product .

Details and Options

Product[f,{i,i_max}] can be entered as 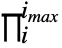f.
∏ can be entered as prod or \[Product].
Product[f,{i,i_min,i_max}] can be entered as 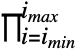f.
The limits should be underscripts and overscripts of ∏ in normal input, and subscripts and superscripts when embedded in other text.
Product uses the standard Wolfram Language iteration specification.
The iteration variable i is treated as local, effectively using Block.
If the range of a product is finite, i is typically assigned a sequence of values, with f being evaluated for each one.
In multiple products, the range of the outermost variable is given first.
The limits of a product need not be numbers. They can be Infinity or symbolic expressions.
If a product cannot be carried out explicitly by multiplying a finite number of terms, Product will attempt to find a symbolic result. In this case, f is first evaluated symbolically.
The indefinite product 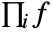is defined so that the ratio of terms with successive gives .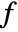
Definite and indefinite summation can be mixed in any order.
The following options can be given:

Assumptions	$Assumptions	assumptions to make about parameters
GenerateConditions	False	whether to generate answers that involve conditions on parameters
GeneratedParameters	None	how to name generated parameters
Method	Automatic	method to use
Regularization	None	what regularization to use
VerifyConvergence	True	whether to verify convergence

Possible values for Regularization include: None and "Dirichlet". {reg₁,reg₂,…} specifies different schemes for different variables in a multiple product.
Product can do essentially all products that are given in standard books of tables.
Product is output in StandardForm using ∏.
Parallelize[Product[f,iter]] or ParallelProduct[f,iter] computes Product[f,iter] in parallel on all subkernels. »

Examples

open allclose all

Basic Examples (5)

Numeric product:

Symbolic product:

Use prod to enter ∏ and to enter the lower limit, then for the upper limit:

Infinite product:

Multiple product with product over performed first:

Scope (28)

Basic Uses (9)

A definite product over a finite range:

Use step size 2:

Use a list of elements:

Plot the sequence of partial products:

A multiple product over finite ranges:

Use different step sizes:

Plot a multivariate sequence and the logarithm of its partial products:

The outermost product bounds can depend on inner variables:

Combine a product over lists with standard iteration ranges:

The elements in the iterator list can be any expression:

Compute a product over an infinite range:

Multivariate product over infinite ranges:

Use a symbolic range:

Indefinite products:

The ratio is equivalent to the multiplicand:

The definite product is given as the ratio of indefinite products:

Multivariate indefinite products:

Mixes of indefinite and definite products:

Use GenerateConditions to get the conditions under which the answer is true:

Refine the resulting answer:

Use Assumptions to provide assumptions directly to Product:

Applying N to an unevaluated product effectively uses NProduct:

Special Indefinite Products (10)

Ratios of expressions with a general function:

Indefinite products are unique up to a constant factor:

For exponential functions, products are equivalent to sums :

The results differ by a constant factor:

The product of polynomial functions can always be done in terms of factorial functions:

Products of rational functions can always be represented as rational functions and factorials:

A minimal number of factorial functions will be used:

Hypergeometric term sequences can be represented in terms of BarnesG:

The DiscreteRatio is rational for all hypergeometric term sequences:

Many functions give hypergeometric terms:

Any products of hypergeometric terms are hypergeometric terms:

Their products in general require BarnesG:

Q-polynomial products can always be represented in terms of q-factorial functions:

A q-polynomial is the composition of a polynomial with an exponential:

Products of q-rational functions can always be done in terms of q-rational and q-factorials:

A q-rational function is the composition of a rational function with an exponential:

In general, Root objects are needed:

Polynomials and rational functions of trigonometric functions:

Similarly for hyperbolic functions:

Rational functions raised to a polynomial power:

Floor and Ceiling related functions:

Periodic sequences:

Any function applied to a periodic sequence generates a periodic sequence:

A sequence raised to a periodic exponent:

A periodic sequence raised to a nonperiodic exponent:

Telescoping products:

Special Definite Products (9)

For exponential functions products are equivalent to sums :

Rational products can be represented as factorial functions:

For infinite products, the limit of the multiplicand needs to be 1:

An infinite product may not converge:

Hypergeometric term products can be represented in terms of BarnesG:

Q-polynomial products can be represented in terms of q-factorial functions:

Some products of q-rational functions can be represented as q-rational functions:

But in general they require q-factorial functions:

Products of trigonometric and hyperbolic functions:

Piecewise products can often be reduced to the previous classes:

In other cases, the piecewise part is eventually constant:

Special products:

Telescoping products:

Multiple products:

Generalizations & Extensions (1)

ParallelProduct computes Product in parallel:

Product can be parallelized automatically, effectively using ParallelProduct:

Options (4)

Assumptions (1)

Use Assumptions to study the behavior under different conditions on the parameter:

GenerateConditions (1)

Generate conditions for convergence of an infinite product:

Regularization (1)

The product of all primes is divergent:

Use Regularization to assign a finite value to this product:

VerifyConvergence (1)

The product of all natural numbers is divergent:

Setting VerifyConvergence to False may assign a finite value in such cases:

Applications (6)

Functions Defined by a Product (1)

Many special functions are defined by products, including Factorial:

And BarnesG:

Product Representations for Constants (1)

Many constants can be represented as products including Pi:

Glaisher:

Product Representations for Functions (1)

Weierstrass factorizations for elementary functions:

Approximate Representation Using Lagrange Interpolation (1)

A Lagrange interpolating polynomial:

A Lagrange interpolating polynomial for symbolic values:

A Newton interpolating polynomial for symbolic values:

Optimized Representations from Product (1)

Using a symbolic closed‐form product can provide fast evaluation:

Compare timings of the closed form to procedural evaluation:

Likelihood Functions for Parameter Estimation (1)

Define a likelihood function for a distribution and dataset:

The likelihood function for an ExponentialDistribution for a small dataset:

Find the maximum-likelihood parameter estimator:

Likelihood function for BernoulliDistribution:

Properties & Relations (4)

NProduct will use numerical methods to compute products:

Applying N to an unevaluated product effectively uses NProduct:

DiscreteRatio is the inverse for indefinite products:

Product essentially solves a special difference equation as solved by RSolve:

Possible Issues (2)

A product may not be convergent:

The upper product limit is assumed to be an integer distance from the lower limit:

Use GenerateConditions to get explicit assumptions:

In general, the upper limit is assumed to be a multiple of distance from the lower limit:

With GenerateConditions, the assumptions are explicit:

Neat Examples (2)

Answers in terms of Zeta and PolyLog derivatives:

Create a gallery of infinite products:

Top