WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Range
✖
Range

✖
Range[imax]

generates the list {1,2,…,imax}.

✖
Range[imin,imax]

generates the list {imin,…,imax}.

✖
Range[imin,imax,di]

uses step di.

Details

  • The arguments to Range need not be integers.
  • Range starts from imin and successively adds increments of di until the result is greater than imax.
  • Range uses the standard Wolfram Language iteration specification, as applied to a single variable.
  • Range has attribute Listable.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

In[1]:=1
✖
https://wolfram.com/xid/0giumy-u7b
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0giumy-bho
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0giumy-m4k
Out[1]=1

Scope  (6)Survey of the scope of standard use cases

Use a step of 2:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-hgq6k3
Out[1]=1

Use a negative step:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-jt2xj5
Out[1]=1

Use an exact numeric-valued step:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-e1ja
Out[1]=1

Use a machine-number step:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-jb208
Out[1]=1

Use a precision-24 step:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-fzgkgx
Out[1]=1

Range of very large numbers:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-b5jce0
Out[1]=1

Generalizations & Extensions  (2)Generalized and extended use cases

Use a symbolic step:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-bictat
Out[1]=1

Use a list of range specifications:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-h2arin
Out[1]=1

Applications  (4)Sample problems that can be solved with this function

Produce a geometric sequence:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-hms323
Out[1]=1

Form a polynomial from coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-13udw
In[2]:=2
✖
https://wolfram.com/xid/0giumy-e7gevf
Out[2]=2

Form a random permutation:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-i8p4cq
Out[1]=1

Find an inverse permutation:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-lr2wfe
Out[1]=1
In[2]:=2
✖
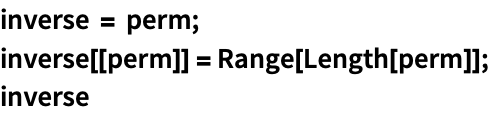
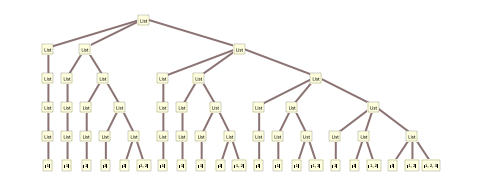
https://wolfram.com/xid/0giumy-ebp95r
Out[2]=2

Properties & Relations  (2)Properties of the function, and connections to other functions

Range[imin,imax,di] is equivalent to Table[i,{imin,imax,di}]:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-h4bg4z
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giumy-jl6j0n
Out[2]=2

Use Range or Span (;;) as Part specification:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-ijkmu8
In[2]:=2
✖
https://wolfram.com/xid/0giumy-czyaw3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giumy-hq1ox0
Out[3]=3

Possible Issues  (3)Common pitfalls and unexpected behavior

For some step sizes, Range may not include the upper limit given:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-efvbkl
Out[1]=1

Even though the lower limit was exact, the inexact step makes the first element inexact:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-bmlol9
Out[1]=1

Range accepts Quantity expressions as limits and steps:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-181vuq
Out[1]=1

For Quantity expressions, Precision is taken into account when determining whether elements are within the bounds of the limits:

In[2]:=2
✖
https://wolfram.com/xid/0giumy-0f5l4n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giumy-rb5j1t
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giumy-d72sge
Out[4]=4

Neat Examples  (1)Surprising or curious use cases

Make nested ranges:

In[1]:=1
✖
https://wolfram.com/xid/0giumy-rw1h1t
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giumy-oo6eae
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giumy-qyjr1
Out[3]=3

Show it in tree form:

In[4]:=4
✖
https://wolfram.com/xid/0giumy-5ivtfo
Wolfram Research (1988), Range, Wolfram Language function, https://reference.wolfram.com/language/ref/Range.html.
✖
Wolfram Research (1988), Range, Wolfram Language function, https://reference.wolfram.com/language/ref/Range.html.

Text

Wolfram Research (1988), Range, Wolfram Language function, https://reference.wolfram.com/language/ref/Range.html.

✖
Wolfram Research (1988), Range, Wolfram Language function, https://reference.wolfram.com/language/ref/Range.html.

CMS

Wolfram Language. 1988. "Range." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Range.html.

✖
Wolfram Language. 1988. "Range." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Range.html.

APA

Wolfram Language. (1988). Range. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Range.html

✖
Wolfram Language. (1988). Range. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Range.html

BibTeX

@misc{reference.wolfram_2025_range, author="Wolfram Research", title="{Range}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Range.html}", note=[Accessed: 01-April-2025 ]}

✖
@misc{reference.wolfram_2025_range, author="Wolfram Research", title="{Range}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Range.html}", note=[Accessed: 01-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_range, organization={Wolfram Research}, title={Range}, year={1988}, url={https://reference.wolfram.com/language/ref/Range.html}, note=[Accessed: 01-April-2025 ]}

✖
@online{reference.wolfram_2025_range, organization={Wolfram Research}, title={Range}, year={1988}, url={https://reference.wolfram.com/language/ref/Range.html}, note=[Accessed: 01-April-2025 ]}