Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ReverseBiorthogonalSplineWavelet

ReverseBiorthogonalSplineWavelet[]

表示阶数为4、对偶阶数为2的逆双正交样条小波.

ReverseBiorthogonalSplineWavelet[n,m]

表示阶数为 n、对偶阶数为 m 的逆双正交样条小波.

更多信息

ReverseBiorthogonalSplineWavelet 定义了双正交小波群.
ReverseBiorthogonalSplineWavelet[n,m] 对正整数 m 和 n 进行定义，其中 m+n 为偶数.
尺度函数 (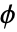) 和小波函数 (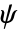) 具有紧支集. 这些函数是对称的.
ReverseBiorthogonalSplineWavelet 可用与函数诸如 DiscreteWaveletTransform 和 WaveletPhi 等一起使用.

范例

打开所有单元关闭所有单元

基本范例 (6)

原尺度函数：

原小波函数：

对偶尺度函数：

对偶小波函数：

原滤波器系数：

对偶滤波器系数：

范围 (17)

基本用途 (10)

计算原低通滤波器系数：

对偶低通滤波器系数：

原高通滤波器系数：

对偶高通滤波器系数：

提升滤波器系数：

产生一个函数计算提升小波变换：

原尺度函数：

对偶尺度函数：

使用不同递归层绘制尺度函数：

原小波函数：

对偶小波函数：

在不同修正尺度上，绘制小波函数：

小波变换 (5)

计算 DiscreteWaveletTransform：

查看小波系数组成的树：

获取小波系数的维度：

绘制小波系数：

计算 DiscreteWaveletPacketTransform：

查看小波系数组成的树：

获取小波系数的维度：

绘制小波系数：

计算一个 StationaryWaveletTransform：

查看小波系数组成的树：

获取小波系数的维度：

绘制小波系数：

计算一个 StationaryWaveletPacketTransform：

查看小波系数组成的树：

获取小波系数的维度：

绘制小波系数：

计算一个 LiftingWaveletTransform：

查看小波系数组成的树：

获取小波系数的维度：

绘制小波系数：

高维度 (2)

多变量尺度函数和小波函数是单变量的积：

多变量对偶尺度函数和小波函数是单变量的积：

属性和关系 (19)

ReverseBiorthogonalSplineWavelet[1,1] 等价于 HaarWavelet：

ReverseBiorthogonalSplineWavelet 等价于 BiorthogonalSplineWavelet ：

ReverseBiorthogonalSplineWavelet 等价于 BiorthogonalSplineWavelet ：

ReverseBiorthogonalSplineWavelet 等价于 BiorthogonalSplineWavelet ：

ReverseBiorthogonalSplineWavelet 等价于 BiorthogonalSplineWavelet ：

低通滤波器系数和为1；：

高通滤波器系数的和为0；：

对偶滤波器系数的和为1；：

对偶高通滤波器系数的和为0；：

尺度函数的积分为1；：

对偶尺度函数的积分为1；：

小波函数的积分为0；：

对偶小波函数的积分为0；：

尺度函数具有紧支集 {n₁,n₂}：

对偶尺度函数具有紧支集 {nd₁,nd₂}：

相应的小波函数具有紧支集 {(n₁– nd₂+1)/2, (n₂– nd₁+1)/2}：

对偶小波函数具有紧支集 {(nd₁– n₂+1)/2, (nd₂– n₁+1)/2}：

满足递归方程：

绘制分量及递归和：

满足递归方程：

绘制分量及递归和：

满足递归方程：

绘制分量及递归和：

满足递归方程：

绘制分量及递归和：

的频率响应由给出：

该滤波器是一个低通滤波器：

的傅立叶变换由给出：

的频率响应由给出：

该滤波器是一个对偶低通滤波器：

的频率响应由给出：

的频率响应由给出：

该滤波器是一个低通滤波器：

的傅立叶变换由给出：

的频率响应由给出：

该滤波器是一个低通滤波器：

的傅立叶变换由给出：

巧妙范例 (2)

绘制尺度函数的平移和伸缩：

绘制小波函数的平移和伸缩：

顶部