WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

SavitzkyGolayMatrix

SavitzkyGolayMatrix[r,k]

次数 k の多項式回帰を行うための，半径 r の平滑化カーネルに相当する行列を与える．

SavitzkyGolayMatrix[{r₁,r₂},{k₁,k₂}]

行に沿った半径 r₁の窓上で次数 k₁の，そして列に沿った半径 r₂の窓上で次数 k₂の，多項式回帰を行うための行列を与える．

SavitzkyGolayMatrix[r,k,n]

次数 k の多項式回帰の n 次微分を行うための行列を与える．

SavitzkyGolayMatrix[{r₁,r₂… },{k₁,k₂,…},…]

各方向 i に指定されたパラメータを使って配列を与える．

詳細とオプション

SavitzkyGolayMatrix[r,k]を使い，局所的多項式回帰を使ってデータを平滑化することができる．
SavitzkyGolayMatrix[r,k,n]を使い，局所的多項式回帰を使ってデータの微分を計算することができる．
SavitzkyGolayMatrix[r,k]の要素の合計は1になる．
SavitzkyGolayMatrixでは，r，k，n の任意のものが，異なる方向について異なる値を指定するリストでよい．
整数 r については，SavitzkyGolayMatrix[r,…]は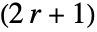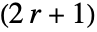，×行列を与える．
非整数 r については，r の値は，事実上，整数に丸められる．
SavitzkyGolayMatrixはWorkingPrecisionオプションを取る．デフォルト設定はWorkingPrecision->MachinePrecisionである．
SavitzkyGolayMatrixは，ListConvolve，ImageConvolve等の関数で用いることができる．

例題

すべて開くすべて閉じる

例 (3)

半径5の窓上で，二次補間についての行列カーネルを計算する：

三次補間を使って長さ11の平滑化カーネルを計算する：

ベクトルをプロットする：

水平次元で一次微分を計算するSavitzky–Golay行列：

スコープ (3)

3D平滑化カーネルを作る：

3D微分カーネル：

一次元に沿った3D微分カーネル：

オプション (1)

WorkingPrecision (1)

デフォルトで，内部計算には機械精度が使われる：

厳密精度を使う：

アプリケーション (2)

2DのSavitzkyGolayMatrixをImageConvolveにおける平滑化カーネルとして使う：

画像の水平微分を計算する：

特性と関係 (1)

多項式の次数は窓のサイズの2倍は超えない：

トップへ