SavitzkyGolayMatrix
SavitzkyGolayMatrix[r,k]
给出对应于半径为 r 的平滑核的矩阵,用于执行度数为 k 的多项式回归.
SavitzkyGolayMatrix[{r1,r2},{k1,k2}]
给出矩阵,用于沿着行在半径为 r1 的窗口上执行度数为 k1 的多项式回归,沿着列在半径为 r2 的窗口上执行度数为 k2 的多项式回归.
SavitzkyGolayMatrix[r,k,n]
给出执行度数为 k 的多项式回归的第 n 阶导数的矩阵.
SavitzkyGolayMatrix[{r1,r2… },{k1,k2,…},…]
使用每个方向 i 的指定参数给出数组.
更多信息和选项

- SavitzkyGolayMatrix[r,k] 可以使用局部多项式回归对数据进行平滑处理.
- SavitzkyGolayMatrix[r,k,n] 可以使用局部多项式回归计算数据的导数.
- SavitzkyGolayMatrix[r,k] 的元素和为1.
- SavitzkyGolayMatrix 允许任意 r、k 和 n 为列表,对不同方向指定不同数值.
- 对于整数 r,SavitzkyGolayMatrix[r,…] 产生一个
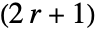 ×
×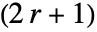 整数.
整数. - 对于非整数 r,r 的数值四舍五入为一个整数.
- SavitzkyGolayMatrix 接受 WorkingPrecision 选项. 默认设置是 WorkingPrecision->MachinePrecision.
- SavitzkyGolayMatrix 可用于诸如 ListConvolve 和 ImageConvolve 的函数.
范例
打开所有单元关闭所有单元应用 (2)
Wolfram Research (2014),SavitzkyGolayMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SavitzkyGolayMatrix.html.
文本
Wolfram Research (2014),SavitzkyGolayMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SavitzkyGolayMatrix.html.
CMS
Wolfram 语言. 2014. "SavitzkyGolayMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SavitzkyGolayMatrix.html.
APA
Wolfram 语言. (2014). SavitzkyGolayMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SavitzkyGolayMatrix.html 年