SchrodingerPDEComponent
SchrodingerPDEComponent[vars,pars]
モデル変数 vars,モデルパラメータ pars のシュレディンガー(Schrödinger)PDE(偏微分方程式)項を与える.
詳細



- 固有系および時間に依存する解析で使用するシュレディンガー方程式を生成する.変数とパラメータを与えるとPDE演算子が返される.
- SchrodingerPDEComponentは,ニュートンの第2法則に類似した非相対論的量子力学であり,量子力学における波動関数の時間発展を記述する.
- SchrodingerPDEComponentは偏微分方程式の一部として使われる微分演算子の和を返す.
- SchrodingerPDEComponentを使って,独立変数
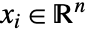 (単位:
(単位:![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/3.png) ),従属変数
),従属変数 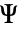 (単位:
(単位:![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2) TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2)](Files/SchrodingerPDEComponent.ja/5.png) ),時間変数
),時間変数 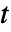 (単位:
(単位:![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/7.png) )でシュレディンガー方程式がモデル化できる.
)でシュレディンガー方程式がモデル化できる. - 定常モデル変数 vars は vars={Ψ[x1,…,xn],{x1,…,xn}}である.
- 時間依存モデル変数 vars は vars={Ψ[t,x1,…,xn],t,{x1,…,xn}}である.
- SchrodingerPDEComponentは運動項とポテンシャル項に基づく.
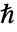 は換算プランク定数(単位:
は換算プランク定数(単位:![TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF]](Files/SchrodingerPDEComponent.ja/10.png) ),
),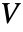 はシュレディンガーポテンシャル(単位:
はシュレディンガーポテンシャル(単位:![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/12.png) )である.
)である. - 質量
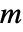 等方性または異方性でよい.
等方性または異方性でよい.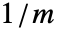 は,以下で与え荒れる
は,以下で与え荒れる 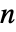 x
x 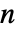 行列を表す.
行列を表す. - 磁場の相互作用について,SchrodingerPDEComponentは以下のようになる.
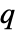 はポテンシャルの粒子の電荷(単位:クーロン,
はポテンシャルの粒子の電荷(単位:クーロン,![TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/20.png) )を表す.
)を表す.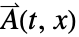 は,
は,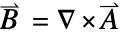 として定義された磁気ベクトルポテンシャル(単位:
として定義された磁気ベクトルポテンシャル(単位:![TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF]](Files/SchrodingerPDEComponent.ja/23.png) )である.ここで,
)である.ここで,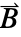 は磁束密度(単位:
は磁束密度(単位:![TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/25.png) )である.
)である.- シュレディンガーPDE項の単位は,波動関数の単位
![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n](Files/SchrodingerPDEComponent.ja/26.png) ジュール(
ジュール(![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.ja/27.png) )倍である.
)倍である. - 次は,使用可能なモデルパラメータ pars である.
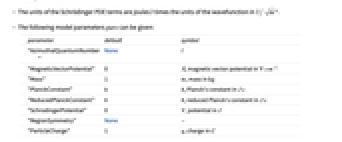
-
パラメータ デフォルト シンボル "AzimuthalQuantumNumber" None 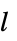
"MagneticVectorPotential" 0 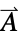 ,磁気ベクトルポテンシャル(単位:
,磁気ベクトルポテンシャル(単位: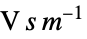 )
)"Mass" 1 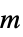 ,質量(単位:
,質量(単位: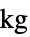 )
)"PlanckConstant" 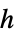
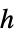 ,プランク定数(単位:
,プランク定数(単位: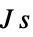 )
)"ReducedPlanckConstant" 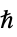
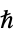 ,換算プランク定数(単位:
,換算プランク定数(単位: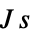 )
)"SchrodingerPotential" 0 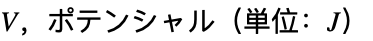
"RegionSymmetry" None 
"ParticleCharge" 1 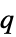 ,電荷(単位:
,電荷(単位: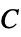 )
) - パラメータはどれも,任意の
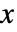 ,
,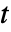 あるいは
あるいは 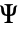 ,または他の従属変数に依存することがある.
,または他の従属変数に依存することがある. - 単位付きのパラメータはSI基本単位に変換される.
- プランク定数および換算プランク定数のデフォルト値の単位はSI基本単位である.
- パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,円筒座標が以下のように角変数を削減することで換算された切頭円筒座標系を表す.
-
次元 削減 一般的な方程式 1D 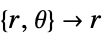
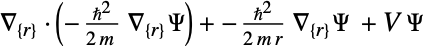
2D 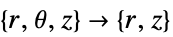
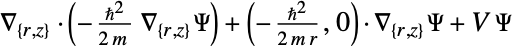
- "RegionSymmetry"が"Axisymmetric"に設定されているときは,
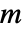 は等方性でなければならない.
は等方性でなければならない. - "AzimuthalQuantumNumber"
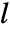 のとき,SchrodingerPDEComponentはいかのようになる.
のとき,SchrodingerPDEComponentはいかのようになる. - 拡散成分はNeumannValueの意味に影響する.
- SchrodingerPDEComponentが連想 pars で…,keypi…,pivi,…として指定されるパラメータ
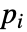 に依存するなら,パラメータ
に依存するなら,パラメータ 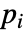 は
は 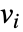 に置換される.
に置換される.
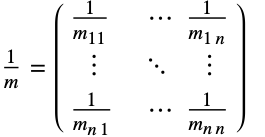
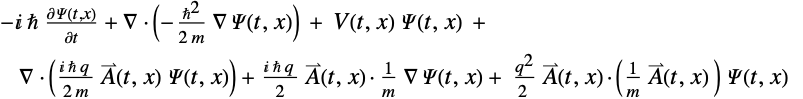
例題
すべて開くすべて閉じる例 (3)
スコープ (16)
1D (6)
3D (2)
軸対称 (3)
アプリケーション (12)
プランク定数1,質量1,ポテンシャル![]() で,時間独立シュレディンガーPDE演算子の固有系を計算する:
で,時間独立シュレディンガーPDE演算子の固有系を計算する:
最も小さい10個の固有値と固有関数を,換算プランク定数 ![]() と
と ![]() の負の値について
の負の値について![]() ,
,![]() の正の値について
の正の値について![]() である区分ポテンシャルで求める.
である区分ポテンシャルで求める.
微細メッシュ上で最も小さい10個の固有値と固有関数を求める:
![]() でスケールされそれぞれの固有値でオフセットされた固有関数を可視化する:
でスケールされそれぞれの固有値でオフセットされた固有関数を可視化する:
円板の中心を通る軸についての対称性を仮定して,半径 ![]() の二次元円板内に閉じ込められた粒子を記述する.粒子についての波動関数は極座標に依存しないと仮定する.
の二次元円板内に閉じ込められた粒子を記述する.粒子についての波動関数は極座標に依存しないと仮定する.
軸対称シュレディンガーPDE演算子をプランク定数![]() で設定する:
で設定する:
領域の外のポテンシャルエネルギーは無限なので,波動関数は境界で消失する.
波動関数が次のように分離できるモデルについて考える.![]() ただし,
ただし,![]() ,
, ![]() ,
, ![]() はそれぞれ円筒座標系の,ラジアル,方位角,高さの座標である.ここで,
はそれぞれ円筒座標系の,ラジアル,方位角,高さの座標である.ここで,![]() は方位量子数である.
は方位量子数である.
この特定の例では無限のポテンシャル壁を持つトーラスに閉じ込められた粒子について考える.これらを考慮すると,トーラスの断面で ![]() を解くことのみが必要になる.
を解くことのみが必要になる.
トーラスの境界で波動関数が消失するような境界条件を定義する:
ヘルパー関数を作成し,方位量子数の異なる値について6つの固有状態を求める.単純化したモデルについてのPDE演算子は ![]() および
および ![]() ,トーラス内の粒子について
,トーラス内の粒子について ![]() である:
である:
方位量子数の値によってエネルギーレベルがどのように変化するかを探索することができる.これを例示するために,![]() についてのエネルギーを0から5まで計算する.
についてのエネルギーを0から5まで計算する.
![]() が大きくなるにつれてエネルギーレベルが非線形的に大きくなる様子を観察する.また,基底状態は非縮退であるのに対し,状態2と3および状態4と5は二重に縮退していることが分かる.
が大きくなるにつれてエネルギーレベルが非線形的に大きくなる様子を観察する.また,基底状態は非縮退であるのに対し,状態2と3および状態4と5は二重に縮退していることが分かる.
波動関数に対する方位量子数の影響を探索するために,総波動関数 ![]() の実部と虚部をプロットする.そのために,
の実部と虚部をプロットする.そのために,![]() の任意の値(例:
の任意の値(例:![]() )を選ぶことができる.
)を選ぶことができる.
量子ビリヤード系,特に2DのBunimovichスタジアムに閉じ込められた粒子が研究できる.
領域の外側のポテンシャルエネルギーが無限だとすると,波動関数は境界で消失する.
時間依存シュレーディンガーPDE演算子を換算プランク定数で設定する:
解をAnimateする:
時間依存シュレディンガーPDE演算子を調和ポテンシャルで設定する:
ポテンシャルを![]() にスケールダウンして確率密度をAnimateする:
にスケールダウンして確率密度をAnimateする:
時間依存シュレディンガーPDE演算子を,換算プランク定数とガウス型ポテンシャル ![]() で設定する:
で設定する:
これをプロットに収まるように![]() にスケールダウンされたポテンシャルとともに可視化する:
にスケールダウンされたポテンシャルとともに可視化する:
解を可視化する.垂直軸と水平軸はそれぞれ時間 ![]() と位置
と位置 ![]() を表す:
を表す:
![]() あたりで波がこの壁に詰め込まれ,反射されることに注意のこと.
あたりで波がこの壁に詰め込まれ,反射されることに注意のこと.
![]() 方向を向いている磁場内の回転なしの荷電粒子がモデル化できる.粒子は初期波束で記述できる.目的は,磁場の相互作用下での確率密度の変化の研究である.これは磁場にある荷電粒子なので,その確率密度は古典的な荷電粒子の挙動と同様,ある種の円軌道を反映すると予想できる.そのため,サイクロトロンの半径がオングストロームのオーダーになるように,非常に高い磁束密度が選択されている.
方向を向いている磁場内の回転なしの荷電粒子がモデル化できる.粒子は初期波束で記述できる.目的は,磁場の相互作用下での確率密度の変化の研究である.これは磁場にある荷電粒子なので,その確率密度は古典的な荷電粒子の挙動と同様,ある種の円軌道を反映すると予想できる.そのため,サイクロトロンの半径がオングストロームのオーダーになるように,非常に高い磁束密度が選択されている.
換算プランク定数,粒子の質量,磁束密度,粒子の電荷をそれぞれ設定する:
粒子の初期条件は運動量が ![]() の,つまり,磁場の相互作用がなければ直進する,波束で記述される.
の,つまり,磁場の相互作用がなければ直進する,波束で記述される.
磁束密度はオングストロームのオーダーのサイクロトロン半径を持つように選ばれる.
長さの単位はオングストローム(![]() )なので,PDE演算子を定義する際はこれを考慮しなければならない.そのため,SchrodingerPDEComponentのパラメータの引数として"ScaleUnits" -> {"Meters" -> "Angstroms"}が使われる.
)なので,PDE演算子を定義する際はこれを考慮しなければならない.そのため,SchrodingerPDEComponentのパラメータの引数として"ScaleUnits" -> {"Meters" -> "Angstroms"}が使われる.
磁気ベクトルポテンシャルのクーロンゲージを仮定するシュレディンガーPDE演算子を定義する:
NeumannValueで透過的な境界条件を持つ問題を解く:
Aharonov–Bohm効果を示すために,磁気ベクトルポテンシャルの影響下で2つのスリットを通過する波束の散乱過程をモデル化する.磁束密度は解析領域全体ではゼロだが,磁気ベクトルポテンシャルはゼロではないことに注意のこと.
例えば,領域は2つのスリットと内部に磁束密度を生成する長いソレノイドを表す小さな穴で定義され,その結果,領域の残りの部分全体に磁気ベクトルポテンシャル場が生成される.波動関数は,磁束密度がゼロではない領域とは相互作用できないことに注意のこと.
一般的な半導体材料である![]() の重い正孔の有効質量の値を使用して,質量が非等方性となるように変数とパラメータを定義する.ここで,"MagneticVectorPotential"パラメータは,磁束密度が
の重い正孔の有効質量の値を使用して,質量が非等方性となるように変数とパラメータを定義する.ここで,"MagneticVectorPotential"パラメータは,磁束密度が![]() で半径が
で半径が![]() のソレノイド用で,直交座標に変換される.
のソレノイド用で,直交座標に変換される.
磁場がない場合と比べて干渉パターンがシフトし,非対称になっているこ点に注意のこと.
特性と関係 (3)
質量 ![]() ,ポテンシャル
,ポテンシャル ![]() の粒子の演算子換算プランク定数
の粒子の演算子換算プランク定数 ![]() で指定する:
で指定する:
パラメータが単位付きで与えられている場合,それらは自動的にSI基本単位に変換される.
拡散係数における各単位系間の違いを調べる.プランク定数割る電子質量を計算する:
以下の例は,内部界面でBenDaniel–Duke境界条件が自動的に適用されることを示している.
幅 ![]() ,有限ポテンシャル
,有限ポテンシャル ![]() ,波動関数
,波動関数 ![]() の量子井戸について考える.井戸の中の粒子の質量は
の量子井戸について考える.井戸の中の粒子の質量は ![]() で障壁領域の粒子の質量は
で障壁領域の粒子の質量は ![]() である.したがって,質量は位置
である.したがって,質量は位置 ![]() の関数である.数量
の関数である.数量 ![]() と
と ![]() は障壁両機と井戸領域の間の界面で連続的でなければならず,BenDaniel–Duke境界条件はこの界面で適用されなければならない. 実際,BenDaniel–Duke境界条件は界面で自動的に適用される.
は障壁両機と井戸領域の間の界面で連続的でなければならず,BenDaniel–Duke境界条件はこの界面で適用されなければならない. 実際,BenDaniel–Duke境界条件は界面で自動的に適用される.
井戸の領域の長さ ![]() の単位はオングストロームであることに注意のこと.PDE演算子を定義するためにパラメータ"ScaleUnits"->{"Meters"->"Angstroms"}が使用される.これによってすべての長さの単位がオングストロームになるようにモデルの残りの量が変換され,数値解の質が向上する.
の単位はオングストロームであることに注意のこと.PDE演算子を定義するためにパラメータ"ScaleUnits"->{"Meters"->"Angstroms"}が使用される.これによってすべての長さの単位がオングストロームになるようにモデルの残りの量が変換され,数値解の質が向上する.
物理的には,波動関数は無限大のすべての束縛状態で![]() になるまで減衰するはずである.実際のモデリングアプローチは,外部境界で
になるまで減衰するはずである.実際のモデリングアプローチは,外部境界で ![]() のディリクレ境界条件を使用する.この境界条件は,量子井戸の中心から十分に長い距離に配置されるようにヒューリスティックに選択される.この場合,距離
のディリクレ境界条件を使用する.この境界条件は,量子井戸の中心から十分に長い距離に配置されるようにヒューリスティックに選択される.この場合,距離 ![]() がこの目的に適している.
がこの目的に適している.
細分化メッシュ上でNDEigensystemを使って固有値問題を解く:
メートル単位がパラメータでオングストロームにスケーリングされたと仮定すると,固有値の単位は![]() である.これを知ることで,固有値を目的のエネルギー単位に変換できる.
である.これを知ることで,固有値を目的のエネルギー単位に変換できる.
最後に,数値的アプローチと解析的アプローチでエネルギー固有値と確率密度を比較することができる.
上記は,BenDaniel–Duke境界条件が実装されている場合,NDEigensystemによって提供されるエネルギー固有値がシュレーディンガー方程式の解析解と数値的に同じであることを示した.さらに,NDEigensystemによって得られる波動関数も解析解と等価である.これは,数値計算手順によって波動関数 ![]() と量
と量![]() の両方の連続性が保証されるためである.
の両方の連続性が保証されるためである.
おもしろい例題 (1)
変数とパラメータを,質量と換算プランク定数![]() で,簡約したシュレディンガーPDE演算子について設定する:
で,簡約したシュレディンガーPDE演算子について設定する:
NDEigensystemを使って一次元時間独立シュレディンガー方程式を解く.この可視化の目的は,バリアの高さと井戸の長さが固有状態に与える影響を確認することである.井戸の長さを伸ばすと各波動関数のエネルギーがどのように減少するかが分かる.一方で,バリアの高さを増すとエネルギーの固有値も大きくなる.
ポテンシャルバリア,井戸の幅,あるいは固有状態の数の任意の値について固有状態を計算する関数を定義する:
Manipulateを設定する:
テキスト
Wolfram Research (2024), SchrodingerPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html (2024年に更新).
CMS
Wolfram Language. 2024. "SchrodingerPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html.
APA
Wolfram Language. (2024). SchrodingerPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html