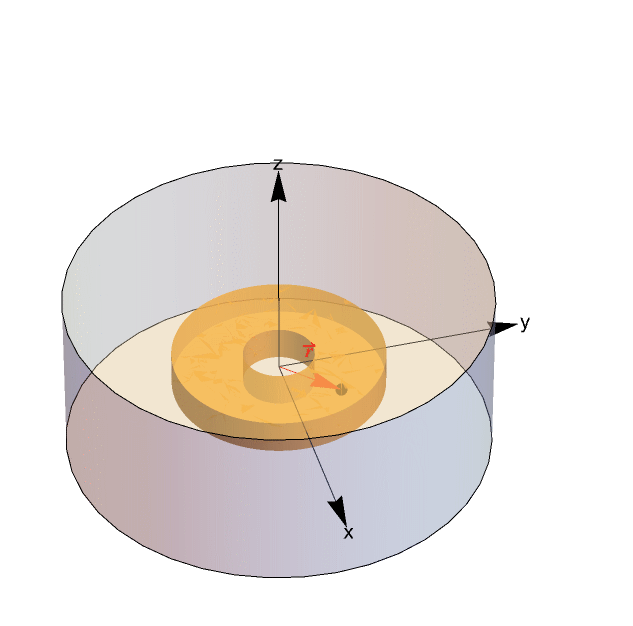
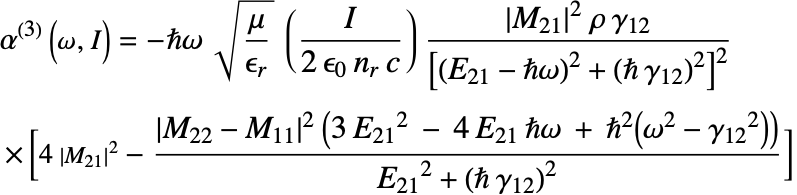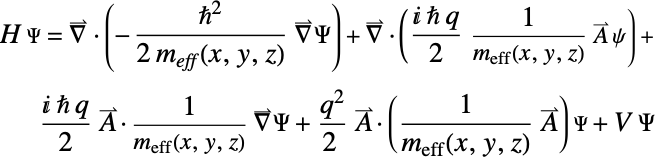Quantum Ring
Introduction
Semiconductor quantum dots (QDs) [Garcia, 2021] are structures made from the union of two or more semiconductor materials, like 
or 
, and are fabricated so their geometry has dimensions on the order of 100 nanometers or less. Due to the difference in energy gaps between each of the semiconductor materials forming the QD, they restrict the mobility of charge carriers like electrons or holes in all three dimensions and, effectively, confine them inside the QD. They exhibit properties that are normally associated with atoms, such as quantized energy levels. For this reason, QDs are sometimes called artificially fabricated atoms. The nature of the charge carriers confined inside QDs is described by the wavefunction that is obtained by solving the Schrödinger equation.
Quantum rings (QRs) are a type of QD that were first fabricated by Granados et al. [Granados, 2003] in 2003. Since their appearance, QRs have been a focus of many condensed matter physicists. They have been proven to be useful in many applications, like lasers [Cao, 2005], quantum computing [Yu, 2008] and single-photon emission [Gallardo, 2010], and there are still other studies that show promising qualities for other applications like optoelectronics [Fomin, 2014].
In many of the studies in the literature, the authors consider two-dimensional QRs like the one by Xie [Xie, 2009], but very few consider the 3D nature of the QRs. This represents one of the advantages that the finite element method has for solving the Schrödinger equation in QDs with rich 3D geometry like QRs.
In this example, a mono-electronic system confined in a quantum ring is considered. The ring is composed of 
, while the surroundings are made of 
. The objective is to find the eigenstates, which can be the starting point for further calculations like optical absorption and thermodynamical properties, among others.
An electron inside the QR will experience a finite step confinement potential, which means that inside the ring, the potential would be 0, and a finite constant potential outside the ring. In standard conditions of pressure and temperature, the potential outside the QR would be of 256.8 meV, when the concentration aluminum is 
[Culchac, 2009].
Depiction of the quantum ring and its surroundings. Here the 
vector represents the position of the electron in the Schrödinger equation.
The behavior of charge carriers inside a crystalline semiconductor, like an electron or a hole, is described by the theory of solid-state physics [Ashcroft, 1976]. In particular, the motion of these particles is described by band theory [Zawadzki, 2020]. In this context, a quantity that is analogous to the electron mass is defined. It is called the effective mass, and it helps describe how a particle in a periodic potential, such as an electron in a crystal, would respond to external forces, taking into account all the interactions that the particle is submitted to inside the crystal. This is a topic with many nuances, for instance, see [Chang, 2014][Duque-Gomez, 2012].
Generally speaking, the effective mass can depend on position and other factors such as temperature and pressure. For this example, as a first approach, a simplification widely used in the literature can be considered. This simplification states that for electrons or holes with a small crystal momentum, the effective mass can be regarded as constant [Zawadzki, 2020]. According to Kohn and Sham [Kohn-Sham, 1965], the numerous interactions within the crystal that each electron experiences can be approximated by a single average potential. This transforms a many-electron problem into a one-electron Schrödinger equation. Additionally, the envelope function approximation can be applied [Harrison, 2005], allowing the time-independent Schrödinger equation for the electron's wavefunction to be written as in equation 1.
The time-independent Schrödinger equation for the electron's wavefunction is given as:
Here 
represents the effective mass of the electron. For 
, 
, 
being the free electron's mass. Also in this case, the potential 
is a piecewise function that defines a potential energy of 
outside the ring and 
inside it.
Parameters
The ring's mean radius 
, width 
, height of the ring 
, boundary radius 
and the height of the whole region 
are defined, which all represent distances in nanometers.
These geometric parameters for this example are inspired by similar theoretical work considering a square cross section quantum ring [Hernandez, 2022].
Domain
It is necessary to load the NDSolve FEM package.
One region is created for the ring and another for the bounding domain.
Next, a region is created by taking the difference between the two regions created above. This results in a hollow part inside the domain, which will define the ring in the mesh later on.
For generating the mesh, the "RegionMarker" option is used to set different mesh element sizes in the two different regions, as well as "RegionHoles"->None, such that ring is part of the mesh too.
Hamiltonian and Confinement Potential
Potential
A finite step potential is defined such that the potential energy is 
outside the ring and 
inside it. The value of the potential is given without units for now, and units will be incorporated later when defining the Hamiltonian.
The SetDelayed statement does not evaluate the right-hand side; as a consequence, in every call to the function V, the ringMemberFunction will need to be evaluated. That makes the process of solving the differential equation inefficient. So, the Evaluate function is used in the definition of the potential to make the whole process more efficient. Consider reading this section on efficient evaluation of PDE coefficients for more details.
Hamiltonian
First, the effective mass and the reduced Planck constant are defined.
Next, the units of the potential are specified with the Quantity function. Since the dimensions of the geometry are in nanometers, the parameter "ScaleUnits"{"Meters""Nanometers"} is set so that all units are consistent.
In the next step, the Schrödinger PDE component is used to generate all the PDE terms.
Boundary Conditions
One Dirichlet condition is imposed, requiring the electron's wavefunction for the low-lying states of interest to decay to 
at a significant distance from the ring. This is achieved by setting the wavefunction to 
at the outer boundary of the previously defined domain.
Solving the Eigenvalue Problem
Now, NDEigensystem is used to solve the eigenvalue problem with the Hamiltonian 
and the mesh previously defined. The variables en and funs are defined as the energy eigenvalues and the wavefunctions, respectively.
It takes less than 
minute to find 
eigenstates with a normal laptop.
Visualization
To interpret the units of the eigenvalues, it is essential to note that the SchrodingerPDEComponent internally converts all units to SI units. When specifying "ScaleUnits"{"Meters""Nanometers"} in the parameters pars, all units of meters are converted to nanometers. Thus, the reverse procedure is followed to convert back to millielectronvolts.
It is clear that the second and third eigenvalues are numerically identical, and the same goes for the fourth and fifth values. This makes sense because these are degenerate eigenstates. Degenerate eigenvalues are expected when the system has symmetry, like the rotational symmetry of the quantum ring. This is easier to see by looking at the corresponding probability densities.
The probability density for the second and third states is basically the same but rotated around the 
axis, as can be seen from the top view. This is because states 
and 
, as well as 
and 
, form a degenerate subspace, meaning that any linear combination of those states would lead to a valid solution.
Also, one important feature is that by making use of NDEigensystem, one obtains the wavefunctions already normalized.
On the other hand, it is possible to take a closer look at each eigenfunction by doing a contour plot.
Magnetic Field Interaction
The effect of an external magnetic field on the eigenstates describing particles confined in low-dimensional systems, such as QDs and QRs, is something that has been considered by various authors [Jahan, 2018], [Gutiérrez, 2010]. One of the reasons this is an area of interest is that the interaction with the magnetic field can greatly affect the energy spectrum and as a consequence, the transition energy between the states confined in the nanostructure. Also, a periodic oscillation in the eigenvalues for each state as the magnetic flux density is increased can be observed, a phenomenon known as Aharanov–Bohm (AB) oscillations. In particular, AB oscillations are present for particles confined in a QR submitted to the presence of a threading magnetic field [Fomin, 2018]. For this reason, an external constant magnetic field pointing in the 
direction will be considered.
Usually, the Hamiltonian operator for a particle of mass 
has the following form: 
, where 
is the momentum operator that in quantum mechanics is defined as 
. On the other hand, by following what is known as Peierl's substitution [Luttinger, 1951][Peierls, 1997], when a magnetic field is present, the momentum changes from 
to 
, where 
is the magnetic vector potential, which is defined in such a way that one can obtain the magnetic flux density as 
.
Therefore, the Hamiltonian takes the following form:
The term 
can be expanded as 
, and therefore, the Hamiltonian would take the form in equation 2.
Now, applying the definition of 
, replacing 
for the effective mass and 
for the electron's charge, the PDE operator acquires the following form.
One particular characteristic of the magnetic vector potential is that one can add the gradient of a scalar function, for instance 
, to 
as 
, and it would lead to the same magnetic flux density, since 
. The function 
is called a gauge function, and choosing a particular 
and 
is called gauge fixing. This choice can, in many cases, lead to a simplification of the equations involved. One common way to do this is to use Coulomb's gauge fixing condition, which states that 
.
As a justification of this condition, consider an original vector potential, 
, which divergence does not make vanish, i.e 
. Then add to it the gradient of a scalar function such that 
. This way, Coulomb's condition, 
, would lead to the equation 
. This is a Poisson-type equation and it has a unique solution. Therefore, 
would be uniquely determined by applying the condition 
. That means that Coulomb's gauge fixing condition can always be applied without any ambiguity. In summary, since the curl of 
is specified by 
but the divergence of 
is not specified, it is possible to set the divergence of 
in a way that simplifies the equations, in this case 
.
Considering Coulomb's gauge fixing condition, the PDE operator can be written as shown in equation 3:
A magnetic vector potential is considered that satisfies the condition that 
, where 
is the position vector, which ensures that 
is true. Then the SchrodingerPDEComponent is used to generate the new PDE operator.
Note that QuantityMagnitude is used in order to ensure that the SchrodingerPDEComponent can handle correctly the units of 
.
To generate the PDE operator, specify the magnetic vector potential and the charge of the particle in the parameters argument of the SchrodingerPDEComponent function. This way, two additional terms are added to the PDE.
Activate was used to show how ultimately the PDE operator given by the SchrodingerPDEComponent is consistent with equation 4.
Note that the Coulomb's gauge for the magnetic vector potential, i.e 
, is satisfied by the specific selection of 
.
Solving the Eigenvalue Problem
Next, the eigenvalue problem can be solved using the same mesh and boundary conditions as before.
Visualization
The presence of the magnetic field makes the wavefunctions complex valued, and it is necessary to separate the real and imaginary parts of the resulting interpolating function to plot it using the Abs function.
The obtained eigenvalues are complex numbers, as the PDE is now complex valued in nature.
Upon close inspection, one can see that the imaginary part is very small compared with the real part, and one can suspect that this is due to numerical noise, given the fact that in quantum mechanics the energy eigenvalues are always a real quantity. For this reason, the real part of the eigenvalues obtained with NDEigensystem will be considered.
Comparing the real part of the eigenvalues with and without the magnetic field reveals that states 
and 
, as well as 
and 
, are no longer degenerate. Thus, the presence of the magnetic field removes the degeneracy of the eigenstates observed when no magnetic field was present.
Varying the Magnetic Field
To explore how the external magnetic field affects the energy eigenvalues, the energy of each state can be calculated as a function of the magnetic flux density. This can be done by just redefining the PDE operator and solving the eigenvalue problem for each value of the magnetic flux density. For this purpose, a function is defined.
Then Table is used to find the energy for a range of magnetic flux densities.
This is a lengthy calculation and takes about 
minutes to complete with the current mesh on a normal laptop.
The last graph represents the AB oscillations of the energy levels, as is often referred to in the literature. One important feature is that the degeneracy in the eigenstates that can be seen when no magnetic field is present at 
is revoked by the presence of the magnetic field. The energy levels then begin to split as the magnetic flux density is increased, a phenomenon known as the Zeeman effect. Furthermore, from the graph, it is clear that the energy of the lowest state starts to grow until a point near 
, where subsequently it starts to fall and then increases again at a point near 
. This oscillation is also present for the remaining states. For instance, the energy of the next state starts decreasing until near 
, when it starts to increase up to a point close to 
, from which it falls back again. And a similar pattern is present for higher states.
In summary, a key feature is that that the mere presence of the magnetic field makes the eigenstates no longer degenerate.
On the other hand, something worth noting in the graph is the "anti-crossing" or "avoided crossing" in the energy levels. For instance, take the point close to 
where the eigenvalues for the first two states come really close and seem to "avoid" each other afterward. This is a common feature of quantum systems, when two eigenvalues will not cross when the strength of a perturbation, as is the case of the magnetic field, is increased [Cohen-Tannaoudji, 1992].
To explore the effect that the external field has on the wavefunctions, the probability densities are plotted for a magnetic flux density of 
. The choice of that specific value will be clear later.
Taking into account the steps in which the magnetic flux density was varied in the previous calculation, the wavefunctions and eigenvalues for a magnetic flux density of 
can be obtained.
These last energies are the real part of the eigenvalues provided by NDEigensystem in millielectronvolts.
There are a few things that one can notice here. First, the wavefunctions for states 
and 
have interchanged roles compared with the wavefunctions previously calculated for a magnetic flux density of 
. And the same can be said about states 
and 
. Moreover, the wavefunction for state 
has a morphology that did not appear in the first five states for the 
case. To explain this, its useful to analyze the AB oscillations graph.
The AB oscillations pattern can be understood as a set of displaced parabolas, each representing a state. This way, the energy for a particular eigenstate at 
, with its correspondent wavefunction, will evolve following a parabola. In the case of 
, the probability densities morphologies are the same as in the no magnetic field case, which can be understood by looking at the last figure and noticing that the ordering of the eigenstates is the same for a value of 
as for a 
case. Inversely, for the case with magnetic flux density of 
, the parabolas have intertwined, and as a consequence, the ordering of the eigenstates has changed, which is reflected in the probability densities as described earlier. Furthermore, state 
in the 
case can be traced back, following a parabola, up to the point with a magnetic flux density of 
, and, as can be seen in the previous graph, in that case it would correspond to state 
. That is the reason why in the morphology of the probability density for state 
in the 
case differs from the previously studied cases.
The choice of the specific magnetic flux density of 
is clearer now. Any value between 
and 
would reveal how the states have intertwined and how the wavefunctions have interchanged order due to the presence of the magnetic field, as can be seen in the graph.
Optical Absorption
Once the eigenstates are computed, additional properties such as the optical absorption can be obtained. To calculate the optical absorption, the first two eigenstates obtained for a magnetic flux density of 
are considered.
The presence of a magnetic field will be included in the optical absorption calculation because, without it, states 
and 
are degenerate, which means that the real physical system will be in a linear combination of the two. Therefore, the magnetic field's ability to remove the degeneracy of the eigenstates will be utilized. And in this case, a magnetic flux density of 
will be sufficient to have the first two eigenstates be non-degenerate.
One way to compute the optical absorption is to follow a procedure described by Karabulut et al. [Karabulut, 2005] that is based on the density matrix formalism and perturbation theory. The details on how the interaction with light is modeled are in Karabulut's paper [Karabulut, 2005]. The expressions for the linear optical absorption 
, the nonlinear optical absorption 
and total optical absorption 
that are given in equations 5, 6 and 7, respectively, can then be applied.
Here, 
is the permeability of 
and 
and 
are vacuum and relative electrical permittivity, respectively. The intensity of the incident light beam is 
, and 
is its frequency. The 
is the inverse of the decay time between states 1 and 2, due to the interaction between the system and the environment. 
is the carrier density of states of 
, 
is the refractive index, and 
is the speed of light. 
are the components of the electric dipole matrix defined as 
, where 
is the electron's charge and 
represents the 
coordinate, which is also in the direction in which the incident light beam is polarized. And finally, 
is the difference between the two energy levels considered, 
.
Next, the necessary quantities are defined.
The components of the electric dipole matrix must have units of [
]. But the geometry and the wavefunctions's length units are nanometers. So, to have the correct units, a factor of 
is introduced in the integral above. Also, note that 
is symmetrical.
The other parameters are defined.
A similar intensity as the one used in the work by Xie [Xie, 2009] will be used.
To plot the absorption, a factor of 
is used to have the 
axis be in meV.
In the latter plot, a peak in the optical absorption around the transition energy 
can be observed. This means that the system is better able to absorb optical waves with an energy that can promote the ground state to the first excited state. Also, the absorption has a maximum for a frequency that is in the terahertz range, which can be one of the characteristics to consider about this type of nanostructure in an optoelectronic application.
Variable Effective Mass Model Extension
In the previous approach, the effective mass of the electron in the 
quantum ring was used throughout the whole region. Although this procedure is widely used in the literature, a more appropriate way to solve the problem is to take into account the difference in effective mass in the ring region and the outside region. So, what is commonly known as a BenDaniel–Duke Hamiltonian [BenDaniel, 1966] is defined.
To get the desired PDE operator, start from the momentum definition discussed earlier, 
, where 
is the charge of the particle. Furthermore, to make the Hamiltonian be Hermitian, and given that the Hermitian conjugate of the product of three operators is 
, the following form in equation 8:
Here, 
represents an operator. Then, equation 9:
Now, the effective mass 
is a function of the position, however, still constant in each subregion. Thus, the effective mass will be a piecewise function.
NDSolve can handle PDE coefficients that are position dependent. The only thing that needs to be done is to make use of the piecewise effective mass in the parameters pars, redefine the magnetic flux density and magnetic vector potential and generate a new Hamiltonian. The equation can be solved as before with the same geometry and mesh.
By default, a Hamiltonian with the diffusion term in the BenDaniel–Duke form is generated.
The boundary condition remains the same as before.
It is important to note that the energies have changed and are lower in magnitude than before. To see this more clearly, the energy eigenvalues for each approach are plotted.
Let's explore the difference between the probability densities for the model with constant effective mass with the ones in the BenDaniel–Duke approach.
Now, let's explore now what happens to the absorption.
The absorption behaves in a very similar manner as before. And maximum frequency has changed by an amount close to 
. To compare how the absorption has changed, the two results are plotted.
These graphs illustrate that there are not drastic changes in the absorption. Nevertheless, the absorption coefficients' maxima have decreased and a small redshift can be observed in the peak frequency when the difference in effective masses between regions is considered.
On the other hand, it is also interesting to explore the changes in the eigenfunctions. By looking at the plots of the wavefunctions for each approach, it is difficult to see any difference. Therefore, the integral of the product between an specific eigenstate considering constant effective mass and the same eigenstate considering variable effective mass is calculated.
The integrals are close to unity, which is expected when one calculates the integral of a given eigenstate squared, which makes one suspect that the eigenfunctions did not change much. Also, from the plot of the difference in the probability density for each approach it is clear that the functional form of the probability density stayed the same.
As a conclusion, it is possible to say that the changes in the energy eigenvalues are appreciable, close to 
of the energy of the ground state. The changes in the position of the absorption peak and the maximum absorption value are minor but noticeable. And this small change can be explained by looking at the eigenfunctions: their value and functional form did not change much. That means that the electric dipole moment matrix components did not undergo a huge change, and they are a big part of the absorption expressions used.
For this problem, the use of the BenDaniel–Duke Hamiltonian may be dispensable if one is only interested in optical absorption, but its inclusion in the model can be essential for accurately calculating the energies.
References
1. García de Arquer, F. P., Talapin, D. v., Klimov, V. I., Arakawa, Y., Bayer, M. and Sargent, E. H. (2021). "Semiconductor Quantum Dots: Technological Progress and Future Challenges." Science, 373 (6555). https://doi.org/10.1126/science.aaz8541
2. Granados, D. and Garcia, J. M. (2003). "Customized Nanostructures MBE Growth: From Quantum Dots to Quantum Rings." Journal of Crystal Growth, 251 (1–4), 213–217. https://doi.org/10.1016/S0022-0248(02)02512-5
3. Cao, H., Deng, H., Ling, H., Liu, C., Smagley, V. A., Caldwell, R. B., Smolyakov, G. A., Gray, A. L., Lester, L. F., Eliseev, P. G. and Osiński, M. (2005). "Highly Unidirectional InAsInGaAsGaAs Quantum-Dot Ring Lasers." Applied Physics Letters, 86(20), 1–3. https://doi.org/10.1063/1.1931044
4. Yu, L. and Voskoboynikov, O. (2008). "Ballistic Aharonov–Bohm Quantum Bits and Quantum Gates." Solid State Communications, 145 (9–10), 447–450. https://doi.org/10.1016/J.SSC.2007.12.017
5. Gallardo, E., Martínez, L. J., Nowak, A. K., Sarkar, D., Sanvitto, D., van der Meulen, H. P., Calleja, J. M., Prieto, I., Granados, D., Taboada, A. G., García, J. M. and Postigo, P. A. (2010). "Single-Photon Emission by Semiconductor Quantum Rings in a Photonic Crystal." Journal of the Optical Society of America B, 27(6), A21. https://doi.org/10.1364/JOSAB.27.000A21
6. Fomin, V. M. (2014). Physiscs of Quantum Rings (Vladimir M Fomin, Ed.). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-39197-2
7. Xie, W. (2009). "Absorption Spectra of a Donor Impurity in a Quantum Ring." Physica Status Solidi (b), 246 (6), 1313–1317. https://doi.org/10.1002/pssb.200844349
8. Culchac, F. J., Porras-Montenegro, N. and Latgé, A. (2009). "Hydrostatic Pressure Effects on Electron States in GaAs–(Ga,Al)As Double Quantum Rings." Journal of Applied Physics, 105 (9), 094324. https://doi.org/10.1063/1.3124643
9. Ashcroft, N. W. and Mermin, N. D. (1976). Solid State Physics. Holt, Rinehart and Winston.
10. Zawadzki, W. (2020). "Wave and Uncertainty Properties of Electrons in Crystalline Solids." Physica Status Solidi (B) Basic Research, 257 (6). https://doi.org/10.1002/pssb.201900517
11. Chang, R., Potnis, S., Ramos, R., Zhuang, C., Hallaji, M., Hayat, A., Duque-Gomez, F., Sipe, J. E. and Steinberg, A. M. (2014). "Observing the Onset of Effective Mass." Physical Review Letters, 112 (17), 170404. https://doi.org/10.1103/PhysRevLett.112.170404
12. Duque-Gomez, F. and Sipe, J. E. (2012). "Response of a Particle in a One-Dimensional Lattice to an Applied Force: Dynamics of the Effective Mass." Physical Review A, 85 (5), 053412. https://doi.org/10.1103/PhysRevA.85.053412
13. Kohn, W. and Sham, L. J. (1965). "Self-Consistent Equations Including Exchange and Correlation Effects." Physical Review, 140 (4A), A1133–A1138. https://doi.org/10.1103/PhysRev.140.A1133
14. Harrison, P. (2005). Quantum Wells, Wires and Dots. John Wiley Sons, Ltd. https://doi.org/10.1002/0470010827
15. Hernández, N., López-Doria, R. A., Rivera, I. E. and Fulla, M. R. (2022). "Refractive Index Change of a D+2 Complex in GaAs/AlxGa1−xAs Quantum Ring." Journal of Materials Science, 57 (18), 8417–8424. https://doi.org/10.1007/s10853-021-06763-8
16. Jahan, K. L., Boda, A., Shankar, I. v., Raju, Ch. N. and Chatterjee, A. (2018). "Magnetic Field Effect on the Energy Levels of an Exciton in a GaAs Quantum Dot: Application for Excitonic Lasers." Scientific Reports, 8 (1), 5073. https://doi.org/10.1038/s41598-018-23348-9
17. Gutiérrez, W., García, L. F. and Mikhailov, I. D. (2010). "Coupled Donors in Quantum Ring in a Threading Magnetic Field." Physica E: Low-Dimensional Systems and Nanostructures, 43 (1), 559–566. https://doi.org/https://doi.org/10.1016/j.physe.2010.09.015
18. Fomin, V. M. (2018). "Quantum Ring: A Unique Playground for the Quantum-Mechanical Paradigm," Physics of Quantum Rings. NanoScience and Technology (V. Fomin, ed.), Springer, Cham. https://doi.org/10.1007/978-3-319-95159-1_1
19. Luttinger, J. M. (1951). "The Effect of a Magnetic Field on Electrons in a Periodic Potential." Physical Review, 84 (4), 814–817. https://doi.org/10.1103/PhysRev.84.814
20. Peierls, R. (1997). "On the Theory of the Diamagnetism of Conduction Electrons" (pp. 97–120), Selected Scientific Papers of Sir Rudolf Peierls (R. H. Dalitz and R. Peierls, eds.). World Scientific. https://doi.org/10.1142/9789812795779_0010
21. Feynman, R. P., Leighton, R. B. and Sands, M. (1965). The Feynman Lectures on Physics. Vol. 3. Addison-Wesley. ISBN 0-201-02115-3. https://www.feynmanlectures.caltech.edu/III_12.html#Ch12-S4
22. Cohen-Tannoudji, B. Diu and F. Laloe, “Quantum Mechanics,” John Wiley & Sons, New York, 1977, (Vol. 1), p.409.
23. Karabulut, İ., Ünlü, S. and Şafak, H. (2005). "Calculation of the Changes in the Absorption and Refractive Index for Intersubband Optical Transitions in a Quantum Box." Physica Status Solidi (b), 242(14), 2902–2909. https://doi.org/10.1002/pssb.200541093
24. BenDaniel, D. J. and Duke, C. B. (1966). "Space-Charge Effects on Electron Tunneling." Physical Review, 152 (2), 683–692. https://doi.org/10.1103/PhysRev.152.683