SinIntegral

SinIntegral[z]

正弦積分関数 TemplateBox[{z}, SinIntegral]=int_0^zsin(t)/t dt を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • TemplateBox[{z}, SinIntegral]=int_0^zsin(t)/t dt
  • SinIntegral[z]は，不連続な分枝切断線を持たない 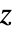の整関数である．
  • 特別な引数の場合，SinIntegralは，自動的に厳密値を計算する．
  • SinIntegralは任意の数値精度で評価できる．
  • SinIntegralは自動的にリストに縫い込まれる．
  • SinIntegralはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (6)

数値的に評価する：

をプロットする：

複素数の部分集合上でプロットする：

を微分する：

原点における級数展開：

Infinityにおける漸近展開：

スコープ  (37)

数値評価  (5)

高精度で数値評価する：

出力の精度は入力の精度に従う：

複素引数について評価する：

SinIntegralを高精度で効率よく評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のSinIntegral関数を計算することもできる：

特定の値  (3)

固定点における値：

無限大における値：

極大値を(dTemplateBox[{x}, SinIntegral])/(dx)=0のコントして求める：

可視化  (2)

SinIntegral関数をプロットする：

TemplateBox[{z}, SinIntegral]の実部をプロットする：

TemplateBox[{z}, SinIntegral]の虚部をプロットする：

関数の特性  (10)

SinIntegralはすべての実数値と複素数値について定義される：

SinIntegralの近似関数の範囲：

SinIntegralは奇関数である：

SinIntegralは x の解析関数である：

SinIntegralは非減少でも非増加でもない：

SinIntegralは単射ではない：

SinIntegralは全射ではない：

SinIntegralは非負でも非正でもない：

SinIntegralは特異点も不連続点も持たない：

SinIntegralは凸でも凹でもない：

微分  (3)

一次導関数：

高次導関数：

次導関数の式：

積分  (3)

SinIntegralの不定積分：

原点を中心とした区間上の奇関数の定積分は0である：

その他の積分例：

級数展開  (4)

SinIntegralのテイラー(Taylor)展開：

の周りのSinIntegralの最初の3つの近似をプロットする：

SinIntegralの級数展開における一般項：

無限大における級数展開を求める：

任意の記号的方向 についての結果を与える：

SinIntegralはベキ級数に適用できる：

関数の恒等式と簡約  (3)

FullSimplifyを使って積分を含む式を簡約する：

式を簡約してSinIntegralにする：

引数の簡約：

関数表現  (4)

SinIntegralの級数表現：

SinIntegralはMeijerGによって表現できる：

SinIntegralはDifferentialRootとして表現できる：

TraditionalFormによる表示：

一般化と拡張  (1)

無限大における級数展開を求める：

任意の記号的方向 についての結果を求める：

アプリケーション  (6)

複素平面で絶対値をプロットする：

オイラー・ハイゼンベルグ(Euler–Heisenberg)の有効作用の実数部分：

の最高次の項を求める：

矩形波についてのギブス(Gibbs)現象：

オーバーシュートの範囲を拡大する：

漸近的なオーバーシュートを計算する：

微分方程式を解く：

三角関数の合成を積分する：

Nielsenの螺線をプロットする：

曲率はパラメータの単純な関数である：

特性と関係  (7)

パリティ変換は自動的に適用される：

FullSimplifyを使って正弦積分を含む式を簡約する：

数値根を求める：

積分と総和からSinIntegralを求める：

微分方程式からSinIntegralを求める：

ロンスキ(Wronski)の行列式を計算する：

Wronskianと比較する：

積分：

ラプラス(Laplace)変換：

考えられる問題  (2)

SinIntegralは中程度の大きさの引数に大きい値を取ることがある：

$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

おもしろい例題  (1)

ネストした積分：

Wolfram Research (1991), SinIntegral, Wolfram言語関数， https://reference.wolfram.com/language/ref/SinIntegral.html （2022年に更新）.

テキスト

Wolfram Research (1991), SinIntegral, Wolfram言語関数， https://reference.wolfram.com/language/ref/SinIntegral.html （2022年に更新）.

CMS

Wolfram Language. 1991. "SinIntegral." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/SinIntegral.html.

APA

Wolfram Language. (1991). SinIntegral. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SinIntegral.html

BibTeX

@misc{reference.wolfram_2024_sinintegral, author="Wolfram Research", title="{SinIntegral}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/SinIntegral.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sinintegral, organization={Wolfram Research}, title={SinIntegral}, year={2022}, url={https://reference.wolfram.com/language/ref/SinIntegral.html}, note=[Accessed: 22-November-2024 ]}