SphericalAngle

SphericalAngle[{θ0,ϕ0}{{θ1,ϕ1},{θ2,ϕ2}}]

点{θ0,ϕ0}と点{θ1,ϕ1}および{θ2,ϕ2}を通る大円の間の符号付きの角度をラジアンで与える．

SphericalAngle[p{q,r}]

n 次元超球面上の点 p，q，r についての符号なしの角度を{θ1,θ2,…,θn-1,ϕ}の形式で与える．

SphericalAngle[p{{q1,r1},…,{qn,rn}}]

点 p から点 qiおよび点 riを通る大円の間の角度のリストを与える．

SphericalAngle[{p1,…,pn}{{q1,r1},…,{qn,rn}}]

点 piから点 qiおよび点 riを通る大円の間の角度のリストを与える．

詳細

  • 球面座標または超球面座標のベクトルは，CoordinateChartDataおよびCoordinateTransformDataと同じ慣習を用いるが，先頭の r 座標は除去される．
  • 大円間の角度はラジアンで計測される．球面や超球面の半径には依存しない．
  • 球面の場合は向きを変えることができるため，符号付きの角度が返される．超球面の場合は，追加の入力がなければ向きを変えることができないため，符号なしの角度が返される．
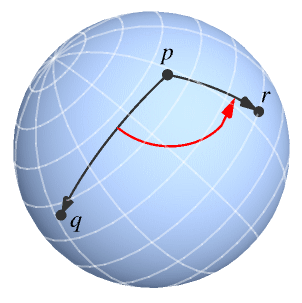
  • 符号規則は，点 p を通る法線の周りで反時計回りに正になる．
  • 2D球面上の点もGeoPosition[{lat,lon}]記法で，緯度と経度は度を単位として指定することができる．
  • SphericalAngleは，数値データを扱う際は複素数値の入力は取らず，実数値の出力だけを返す．

例題

すべて開くすべて閉じる

例  (4)

極大円間の角度を計算する：

三次元球面上の測地線ペアの間の角度を求める：

記号計算を行う：

値の典型的な範囲を仮定して結果を簡約する：

四次元球面上の，すべてが選択した1つの点を中心とする10個のランダムな角度を計算する：

スコープ  (3)

球面上の任意の点の間の記号的な角度を計算する：

四面体の頂点の周りの角度を30桁精度計算する：

厳密値と比較する：

SphericalAngleには，GeoPositionの緯度と経度の座標も使うことができる：

アプリケーション  (1)

球面八分円の3つの境界点を定義する：

各頂点の内角を計算する：

これらの角度の和から π を引いたものは単位球の面積の1/8であることを確認する：

特性と関係  (3)

GeoDirectionは，地球の楕円体モデル上の北極からの角度を計算する：

球面上で同様の角度を計算する：

GeoDirectionが地球の球体モデルを使うように強制する：

バミューダトライアングルの面積を近似する：

地球の楕円体モデルを使うGeoAreaと比較する：

超球面上に3点取る：

SphericalAngleの結果はVectorAngleを使って計算することもできる：

考えられる問題  (1)

p と q が対蹠的なとき，角度 q-p-r は不定である：

Wolfram Research (2024), SphericalAngle, Wolfram言語関数， https://reference.wolfram.com/language/ref/SphericalAngle.html.

テキスト

Wolfram Research (2024), SphericalAngle, Wolfram言語関数， https://reference.wolfram.com/language/ref/SphericalAngle.html.

CMS

Wolfram Language. 2024. "SphericalAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalAngle.html.

APA

Wolfram Language. (2024). SphericalAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SphericalAngle.html

BibTeX

@misc{reference.wolfram_2025_sphericalangle, author="Wolfram Research", title="{SphericalAngle}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SphericalAngle.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_sphericalangle, organization={Wolfram Research}, title={SphericalAngle}, year={2024}, url={https://reference.wolfram.com/language/ref/SphericalAngle.html}, note=[Accessed: 03-April-2025 ]}