VectorAngle[u,v]
gives the angle between the vectors u and v.


VectorAngle
VectorAngle[u,v]
gives the angle between the vectors u and v.
Details
- VectorAngle gives an angle in radians.
- For nonzero real vectors the vector angle
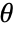 satisfies
satisfies 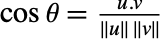 .
. - For complex vectors the numerator is
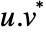 .
.
Examples
open all close allBasic Examples (2)
Scope (2)
Applications (3)
Properties & Relations (6)
The generalization to complex vectors satisfies ![]() :
:
If you rotate a vector u in a plane that includes u, then the vector angle is the rotation angle:
If you rotate it in a plane that does not include u, then the angles differ:
The vector angle ![]() is related to the cross product through
is related to the cross product through ![]() :
:
ArcTan of two arguments gives the signed vector angle between the ![]() axis and the vector:
axis and the vector:
Eigenvectors are the vectors for which the angle between ![]() and
and ![]() is 0:
is 0:
See Also
PlanarAngle PolygonAngle Dot Projection ArcCos Cross Degree CosineDistance
Function Repository: SignedVectorAngle AngleBetweenPlanes
Related Guides
History
Text
Wolfram Research (2007), VectorAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/VectorAngle.html.
CMS
Wolfram Language. 2007. "VectorAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VectorAngle.html.
APA
Wolfram Language. (2007). VectorAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VectorAngle.html
BibTeX
@misc{reference.wolfram_2025_vectorangle, author="Wolfram Research", title="{VectorAngle}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/VectorAngle.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_vectorangle, organization={Wolfram Research}, title={VectorAngle}, year={2007}, url={https://reference.wolfram.com/language/ref/VectorAngle.html}, note=[Accessed: 10-March-2026]}