SphericalAngle

SphericalAngle[{θ0,ϕ0}{{θ1,ϕ1},{θ2,ϕ2}}]

给出通过点 {θ0,ϕ0}、{θ1,ϕ1} 和 {θ2,ϕ2} 的大圆之间的带符号的角，单位为弧度.

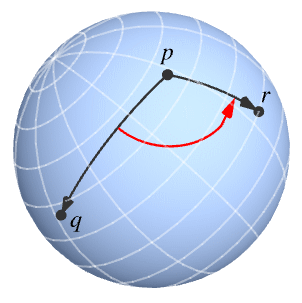
SphericalAngle[p{q,r}]

给出 n 维超球面上形式为 {θ1,θ2,…,θn-1,ϕ} 的点 p、q、r 的无符号角.

SphericalAngle[p{{q1,r1},…,{qn,rn}}]

给出从点 p 出发穿过点 qi 和 ri 的大圆之间的角的列表.

SphericalAngle[{p1,…,pn}{{q1,r1},…,{qn,rn}}]

给出从点 pi 出发穿过点 qi 和 ri 的大圆之间的角的列表.

更多信息

  • 球面或超球面坐标向量使用与 CoordinateChartData 和 CoordinateTransformData 相同的指定方式，但是删除了前面的 r 坐标.
  • 大圆之间的角以弧度为单位，与球面或超球面的半径无关.
  • 球面情况下是可定向的，因此返回带符号的角度. 超球面情况下，在没有额外输入的情况下是不可定向的，因此返回无符号的角度.
  • 符号约定：穿过点 p 的法线的逆时针方向为正.
  • 2D 球面上的点也可以使用 GeoPosition[{lat,lon}] 表示法指定，其中，纬度和经度的单位为度.
  • 处理数值型数据时，SphericalAngle 不接受复数输入，只返回实数输出.

范例

打开所有单元关闭所有单元

基本范例  (4)

计算极地大圆之间的角度：

求 3-球面上一对测地线之间的角度：

执行符号计算：

假设取常见值，简化结果：

计算 4-球面上的 10 个随机角度，所有角度都以一个选定点为中心：

范围  (3)

计算球面上任意点之间的符号角 (symbolic angle)：

使用 30 位精度计算四面体的一个顶点周围的角度：

与精确值比较：

SphericalAngle 也可以接受 GeoPosition 纬度-经度坐标：

应用  (1)

定义包围球面八分圆的三个点：

计算每个顶点的内角：

验证这些角度的总和减去 π 等于单位球面面积的八分之一：

属性和关系  (3)

GeoDirection 计算的是与地球椭球模型上北极之间的角度：

计算球面上的类似角度：

强制 GeoDirection 使用地球的球形模型：

近似计算百慕大三角的面积：

与使用地球椭球模型的 GeoArea 进行比较：

在超球面上取三个点：

也可以使用 VectorAngle 计算 SphericalAngle 的结果：

可能存在的问题  (1)

当 p 和 q 对蹠时，角 q-p-r 是不确定的：

Wolfram Research (2024)，SphericalAngle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SphericalAngle.html.

文本

Wolfram Research (2024)，SphericalAngle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SphericalAngle.html.

CMS

Wolfram 语言. 2024. "SphericalAngle." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalAngle.html.

APA

Wolfram 语言. (2024). SphericalAngle. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SphericalAngle.html 年

BibTeX

@misc{reference.wolfram_2024_sphericalangle, author="Wolfram Research", title="{SphericalAngle}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SphericalAngle.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sphericalangle, organization={Wolfram Research}, title={SphericalAngle}, year={2024}, url={https://reference.wolfram.com/language/ref/SphericalAngle.html}, note=[Accessed: 22-November-2024 ]}