Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

StieltjesGamma

StieltjesGamma[n]

gives the Stieltjes constant .

StieltjesGamma[n,a]

gives the generalized Stieltjes constant .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
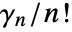is the coefficient of 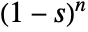in the Laurent expansion of 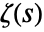about the point .
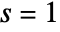The 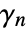are generalizations of Euler's constant; .
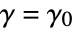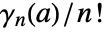is the coefficient of 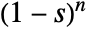in the Laurent expansion of 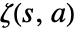about the point .
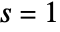For certain special arguments, StieltjesGamma automatically evaluates to exact values.
StieltjesGamma can be evaluated to arbitrary numerical precision.
StieltjesGamma automatically threads over lists.
StieltjesGamma can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples (3)

Evaluate to high precision:

Plot values of StieltjesGamma:

Scope (5)

TraditionalForm formatting:

Evaluate for complex second argument:

The precision of the output tracks the precision of the input:

StieltjesGamma threads element-wise over lists:

StieltjesGamma can be used with Interval and CenteredInterval objects:

Applications (3)

Expansion of the Riemann zeta function:

Expansion of the Hurwitz zeta function:

Test Li’s criterion for the Riemann hypothesis:

All values should be positive:

Express integrals in terms of StieltjesGamma:

Properties & Relations (2)

The EulerGamma case evaluates automatically:

Various symbolic relations are automatically used:

Possible Issues (4)

Substitution of derivatives of Zeta at yields indeterminate values:

Use Limit to obtain the expansion coefficient:

The argument of StieltjesGamma must be an exact non-negative integer:

Use N to obtain a numerical approximation:

Alternatively, use two-argument form:

StieltjesGamma does not allow numericalization of its index:

It is currently not known if Stieltjes constants are algebraic numbers:

Top