SymmetricReduction

SymmetricReduction[f,{x1,…,xn}]

gives a pair of polynomials in such that , where is the symmetric part and is the remainder.

SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]

gives the pair with the elementary symmetric polynomials in replaced by .

Details

  • If 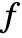f is a symmetric polynomial, then 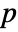is the unique polynomial in elementary symmetric polynomials equal to 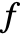f, and 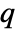is zero.
  • If 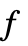f is not a symmetric polynomial, then the output is not unique, but depends on the ordering of its variables.
  • For a given ordering, a nonsymmetric polynomial 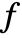f can be expressed uniquely as a sum of its symmetric part 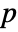and a remainder 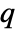that does not contain descending monomials. A monomial 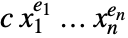is called descending if .
  • Changing the ordering of the variables may produce different pairs .
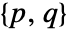  • SymmetricReduction does not check to see that 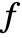f is a polynomial, and will attempt to symmetrize the polynomial part of f.

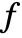Examples

open allclose all

Basic Examples  (3)

Write a symmetric polynomial as a sum of elementary symmetric polynomials:

Write a nonsymmetric polynomial as a symmetric part and a remainder:

Name the first two elementary symmetric polynomials s1 and s2:

Scope  (2)

SymmetricReduction will reduce the polynomial part of an expression:

Applications  (2)

Let the roots of the equation be , , . The coefficients , , are trivially related to the symmetric polynomials of , , :

A similar expression holds for the monic polynomial with roots , , :

Use SymmetricReduction to solve for , , :

The monic polynomial with roots , , :

Check:

Consider solving the following symmetric system of equations:

Use ChebyshevT to convert to a symmetric system of polynomials:

Solve is able to solve the equations in the variables x1,x2,x3:

The leaf count of the solution is enormous:

Convert to a system of equations of symmetric polynomials :

Solve the new system of equations:

The leaf count of the symmetric solution is much smaller:

Solving for the variables x1,x2,x3 in terms of the symmetric polynomials is also quick:

Properties & Relations  (2)

The order of variables can affect the decomposition into symmetric and nonsymmetric parts:

Another basis for the symmetric polynomials consists of the complete symmetric polynomials. They are the sum of all monomials of a given degree, and can be defined by the generating function Product[1-xit,{i,n}]-1:

A determinant formula expresses the elementary symmetric polynomials in the basis of the complete symmetric polynomials:

Check:

Any symmetric polynomial can also be expressed in terms of the complete symmetric polynomials:

Wolfram Research (2007), SymmetricReduction, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricReduction.html.

Text

Wolfram Research (2007), SymmetricReduction, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricReduction.html.

CMS

Wolfram Language. 2007. "SymmetricReduction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricReduction.html.

APA

Wolfram Language. (2007). SymmetricReduction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricReduction.html

BibTeX

@misc{reference.wolfram_2025_symmetricreduction, author="Wolfram Research", title="{SymmetricReduction}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricReduction.html}", note=[Accessed: 30-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_symmetricreduction, organization={Wolfram Research}, title={SymmetricReduction}, year={2007}, url={https://reference.wolfram.com/language/ref/SymmetricReduction.html}, note=[Accessed: 30-July-2025 ]}