SystemsModelLinearity

SystemsModelLinearity[sys]

给出系统模型 sys 的线性度.

SystemsModelLinearity[{sys,{in1,…},{out1,…},{s1,…}}]

只考虑与输入 ini，输出 outj 以及状态 sk 有关的子系统.

更多信息

  • SystemsModelLinearity 通常被用来决定一个 NonlinearStateSpaceModel 或 AffineStateSpaceModel 是否满足附加线性度条件，这让它能被准确转换成一个更加特殊的形式，从而使得更广范围的设计和分析技术能被应用.
  • 可能的系统模型 sys 包括 TransferFunctionModel，StateSpaceModel，AffineStateSpaceModel 及 NonlinearStateSpaceModel.
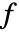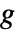  • 可以根据什么变量线性出现在 和 中对状态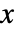为 ，输入为 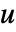，状态方程为 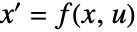、输出方程为 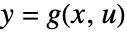的状态空间模型进行分类.
  • 以下给出 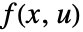和 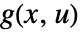必需的可能的值和结构形式：
  • "Linear"在状态和输入里线性，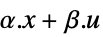
    "Bilinear"在状态和输入里单独线性，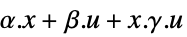
    "StateLinear"只有在状态里线性，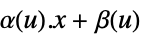
    "InputLinear"只有在输入里线性，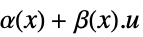
    "Nonlinear"在状态或输入里均不线性

范例

打开所有单元关闭所有单元

基本范例  (2)

线性弹簧-阻尼-质量（MSD）模型：

有立方非线性弹簧的 MSD 模型：

范围  (7)

线性模型：

线性的 NonlinearStateSpaceModel：

双线性模型：

输入-线性模型：

非线性的模型：

频域模型为线性模型：

带有线性状态方程的模型：

应用  (2)

用 StateTransformationLinearize 检验获得的线性化：

检查是否为输入-输出线性：

检查是否为状态-输出线性：

检查是否为输入-状态线性：

计算系统连接后的线性化：

连接串联的两个系统：

原始系统和连接后系统的线性度：

属性和关系  (4)

一个线性系统遵循叠加性和均匀性的原则：

它对输入信号 的响应：

对 TemplateBox[{t}, UnitStepSeq] 的响应：

对 3 sin(t)+5 TemplateBox[{t}, UnitStepSeq] 的响应与 相同：

通常 StateSpaceModel 被用来模拟线性状态-空间模型：

这模型可以被准确的转换成为其他任何系统模型：

通常 AffineStateSpaceModel 可以用于双线性模型和输入-线性模型：

它可以被准确的转换到 NonlinearStateSpaceModel：

到其他系统模型的转换为近似转换：

对于非线性模型，使用 NonlinearStateSpaceModel：

转换成任何其他系统模型是近似的：

Wolfram Research (2014)，SystemsModelLinearity，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

文本

Wolfram Research (2014)，SystemsModelLinearity，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

CMS

Wolfram 语言. 2014. "SystemsModelLinearity." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

APA

Wolfram 语言. (2014). SystemsModelLinearity. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SystemsModelLinearity.html 年

BibTeX

@misc{reference.wolfram_2024_systemsmodellinearity, author="Wolfram Research", title="{SystemsModelLinearity}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelLinearity.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_systemsmodellinearity, organization={Wolfram Research}, title={SystemsModelLinearity}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelLinearity.html}, note=[Accessed: 22-November-2024 ]}