SystemsModelVectorRelativeOrders

SystemsModelVectorRelativeOrders[sys]

系のモデル sys のベクトル相対次数を与える．

詳細とオプション

  • SystemsModelVectorRelativeOrdersはベクトル相対次数として知られている．
  • 相対次数とは，基本的に，系 sys の入力 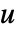が明示的に出現するために，sys の出力 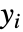が微分されなければならない回数のことである．
  • 出力の 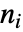回の微分後に 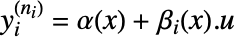が得られるのであれば，出力 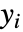の相対次数は 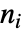である．
  • ベクトル相対次数は，各出力の相対次数のリスト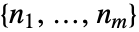である．
  • 行列 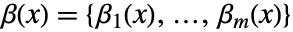はデカップリング行列と呼ばれ，階数 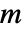であることが必要である．
  • 系 sys は，TransferFunctionModel，StateSpaceModel，あるいはAffineStateSpaceModelでよい．
  • 使用可能なオプション
  • MaxIterationsAutomatic微分の最大回数
    ZeroTestAutomaticゼロテスト

例題

すべて開くすべて閉じる

例  (1)

系のベクトル相対次数を計算する：

スコープ  (4)

単一出力系のベクトル相対次数：

多出力系のベクトル相対次数：

StateSpaceModelのベクトル相対次数：

TransferFunctionModelのベクトル相対次数：

アプリケーション  (2)

フィードバック線形化を施された系と残差系における状態数を決定する：

線形部分系の状態数：

線形化された部分系：

残差部分系の状態数：

残差部分系：

AsymptoticOutputTrackerでは，減衰率は相対次数に基づいて割り当てられる：

最初の3つは第1出力，残りの2つは第2出力に対応する：

第1出力の減衰率は比較的低く，したがって基準入力に続いてのスタートに時間がかかる：

特性と関係  (7)

ベクトル相対次数の長さは出力数に等しい：

SystemsModelDimensionsを使って出力数を求める：

ゼロダイナミクスのないスカラー系については，ベクトル相対次数は次数に等しい：

SystemsModelOrderを使って系の次数を求める：

ベクトル相対次数が有限の場合は，線形化フィードバック制御を計算することができる：

FeedbackLinearizeを使って線形化フィードバックを計算する：

ベクトル相対次数の和が次数と等しい場合は，ゼロダイナミクスはない：

相対次数は，フィードバック線形化系の積分器鎖の長さを与える：

出力1は単一積分器，出力2は二重積分器を持つ：

ベクトル相対次数は座標変換について不変である：

ベクトル相対次数は，伝達関数の漸近次数に相当する：

出力1（第1行）の漸近次数は3，出力2（第2行）の漸近次数は2である：

考えられる問題  (3)

デカップリング行列が可逆になるためには，出力は独立でなければならない：

入力数は少なくとも出力数と等しくなければならない：

操作点が指定されている場合，デカップリング行列はその点で評価される：

この系のフィードバックは線形化されているが，操作点に特異点がある：

Wolfram Research (2014), SystemsModelVectorRelativeOrders, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.

テキスト

Wolfram Research (2014), SystemsModelVectorRelativeOrders, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.

CMS

Wolfram Language. 2014. "SystemsModelVectorRelativeOrders." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.

APA

Wolfram Language. (2014). SystemsModelVectorRelativeOrders. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html

BibTeX

@misc{reference.wolfram_2024_systemsmodelvectorrelativeorders, author="Wolfram Research", title="{SystemsModelVectorRelativeOrders}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_systemsmodelvectorrelativeorders, organization={Wolfram Research}, title={SystemsModelVectorRelativeOrders}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html}, note=[Accessed: 18-November-2024 ]}