SystemsModelVectorRelativeOrders
SystemsModelVectorRelativeOrders[sys]
给出系统模型 sys 的向量相对阶数.
更多信息和选项

- SystemsModelVectorRelativeOrders 也称为向量相对度数.
- sys 的输出
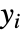 的相对阶数基本上是使 sys 的输出
的相对阶数基本上是使 sys 的输出 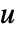 显示出现必须求导的次数t.
显示出现必须求导的次数t. - 输出
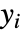 具有相对阶数
具有相对阶数 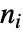 ,如果在对输出
,如果在对输出 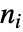 次求导后,
次求导后,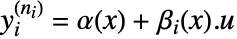 .
. - 向量相对阶数是每个输出的相对阶数的列表
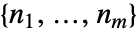 .
. - 矩阵
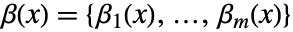 称为解耦矩阵,并且阶数必须为
称为解耦矩阵,并且阶数必须为 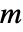 .
. - 系统 sys 可以是 TransferFunctionModel、StateSpaceModel 或者 AffineStateSpaceModel.
- 可以给出下列选项:
-
MaxIterations Automatic 求导数的最大次数 ZeroTest Automatic 零检测
范例
打开所有单元关闭所有单元范围 (4)
应用 (2)
在 AsymptoticOutputTracker 中,基于相关阶指定衰减率:
属性和关系 (7)
Wolfram Research (2014),SystemsModelVectorRelativeOrders,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.
文本
Wolfram Research (2014),SystemsModelVectorRelativeOrders,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.
CMS
Wolfram 语言. 2014. "SystemsModelVectorRelativeOrders." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.
APA
Wolfram 语言. (2014). SystemsModelVectorRelativeOrders. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html 年