TTest

TTest[data]

data の平均が0かどうか調べる．

TTest[{data1,data2}]

data1と data2の平均が等しいかどうか調べる．

TTest[dspec,μ0]

μ0について平均を調べる．

TTest[dspec,μ0,"property"]

"property"の値を返す．

詳細とオプション

  • TTestは帰無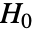仮説 と対立仮説 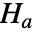で検定を行う．
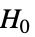
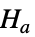
  • data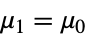
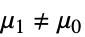
    {data1,data2}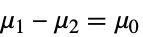
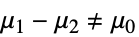
  • ただし，μiは dataiの母平均である．
  • デフォルトで，確率値つまり 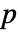値が返される．
  • 小さい 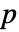値は 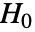が真である可能性が低いことを示す．
  • dspec 中のデータは一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい．
  • 引数 μ0は実数あるいはデータの次元と長さが等しい実ベクトルでよい．
  • TTestはデータが正規分布に従うと仮定するが，この仮定についてかなり強力である．TTestはまた2つのサンプルがある場合はサンプルがそれぞれ独立であると仮定する．
  • TTest[dspec,μ0,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • TTest[dspec,μ0,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定で使用される自由度
    "PValue" 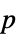値のリスト
    "PValueTable" 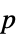値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 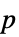値のペアのリスト
    "TestDataTable"検定統計と 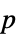値のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 一変量のサンプルの場合，TTestはスチューデント 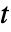検定を行う．検定統計はStudentTDistribution[df]に従うと仮定される．
  • 多変量のサンプルの場合，TTestはHotellingの 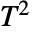検定を行う．検定統計はHotellingTSquareDistribution[p,df]に従うと仮定される．ただし，p は data の次元である．
  • 検定統計の分布指定に使われる自由度 df は，サンプルの大きさ，サンプル数，さらに2つの一変量サンプルの場合は分散が等しいかどうかの検定結果に依存する．
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    SignificanceLevel 0.05診断と報告のための切捨て
    VerifyTestAssumptions Automaticどの仮定を検証するか
  • TTestでは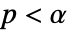， のときにのみ 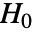が棄却されるような切捨て 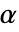が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 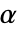の値はSignificanceLevelオプションで制御される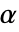． の値は，正規性，等分散，対称性の検定を含む仮定の診断検定にも使われる．デフォルトで 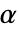は0.05に設定される．
  • TTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Normality"すべてのデータが正規分布に従うことを検証する
    "EqualVariance"data1と data2が等分散であることを検証する

例題

すべて開くすべて閉じる

例  (3)

母集団の平均が0かどうか調べる：

完全な検定表：

2つの母集団の平均の差がかどうか調べる：

平均差分 ：

0.05レベルでは，は2と著しく異なる：

多変量母集団の位置を比較する：

平均差分ベクトル ：

0.05レベルでは，は {1,2}とそれほど違わない：

スコープ  (13)

検定  (10)

対 を検定する：

平均が に近い場合， 値は通常大きい：

位置が から離れている場合， 値は通常小さい：

Automaticを使うことは，ゼロの平均について検定することと同じである：

対 を検定する：

平均が に近い場合， 値は通常大きい：

位置が から離れている場合， 値は通常小さい：

多変量データ集合の平均ベクトルがゼロベクトルであるかどうかを検定する：

{0.1,0,–0.05,0}についても検定する：

対 を検定を行う：

位置が等しくない場合， 値は一般に小さい：

位置が等しい場合， 値は一般に大きい：

対 を検定する：

データ集合の順序は検定結果に影響する：

2つの多変量データ集合の平均差分ベクトルがゼロベクトルであるかどうかを検定する：

{1,0,–1,0}についても検定する：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

HypothesisTestDataオブジェクトから特性を抽出する：

値，検定統計，および自由度：

任意数の特性を同時に抽出する：

値，検定統計，および自由度：

レポート  (3)

検定結果を表にする：

カスタマイズしたレポート用に検定表から項目を取り出す：

値か検定統計を表にする：

表の 値：

表の検定統計：

オプション  (11)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

対 を検定する：

両側検定を行う．あるいは片側検定を代りに行う：

対 を検定する：

対 を検定する：

対 を検定する：

が与えられている場合に，片側検定を代りに行う：

対 を検定する：

対 を検定する：

SignificanceLevel  (2)

診断検定の有意水準を設定する：

デフォルトで0.05が使われる：

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

VerifyTestAssumptions  (6)

デフォルトで正規性と等分散の検定が行われる：

仮定がチェックされない場合，検定結果が異なることがある：

AllあるいはNoneを使ってまとめて診断を制御することができる：

すべての仮定をチェックする：

どの仮定もチェックしない：

診断は個々に制御することができる：

正規性を仮定して，等分散についてチェックする：

正規性についてのみチェックする：

等分散の仮定をFalseに設定する：

リストされていない仮定については検定を行わない：

ここでは正規性が想定されている：

結果は同じであるが，警告メッセージが出される：

診断検定を使わないと，計算時間が短縮できる：

シミュレーションを行う場合は，診断検定を行わないようにすると有益であることが多い：

検定の仮定は意図的に有効になっているので，時間が大幅に短縮できる：

結果は全く同じである：

アプリケーション  (4)

ある母集団の平均が等しいかどうかについて検定を行う：

最初の2つの母集団の平均は似ている：

3つ目の母集団の平均は1つ目のものと異なる：

光の通過速度の3つ目の一連の測定値は，1882年にニューコム(Newcomb)よって記録された．与えられた値を1000で割って24加えたものは，既知の距離を光が移動する時間（単位：100万分の1秒）を与える．現在のところ，真の値は33.02であると考えられている：

ショーブネ(Chauvenet)の基準を使って外れ値を識別する：

データの大部分について 検定を行うと，ニューコムの光速度の測定値は実際の値よりもかなり低いことが分かる：

2つの実験的なキャベツの栽培品種それぞれから30個のサンプルについてビタミンCの量と全体の重さを記録した：

全体の重さとビタミンCの量を栽培品種ごとにプロットする：

ビタミンCの量はc52の栽培品種においてかなり高い：

重さのデータはc52については正規分布に従わないので，MannWhitneyTestを使って軽いキャベツの方がずっと多くのビタミンCを含むことを示す：

アヤメの花の3つの種のそれぞれから50のサンプルが集められた．サンプルは，アヤメの萼片と花弁の長さと幅の測定値からなる．virginica および versicolor の種を区別することは難しい：

Hotelling 検定は，2つの似た種について測定値の違いを示す：

データを可視化すると，最も大きい違いは花弁の大きさであることが分かる：

特性と関係  (11)

一変量データについては，において検定統計はStudentTDistributionに従う：

多変量データについては，において検定統計はHotellingTSquareDistributionに従う：

自由度は一変量データについてはデータに依存する：

1サンプル：

等分散の2つのサンプル：

等しくない分散を持つ2つのサンプル（サタスウェイト(Satterthwaite)近似）：

使用される自由度のタイプはVerifyTestAssumptionsを使って制御できる：

等分散を明示的に仮定して，正規性についての検定を行う：

Satterthwaite近似を使うために明示的に不等分散を仮定する：

多変量データについては，Hotellingの 統計の計算に平方マハラノビス(Mahalanobis)距離が使われる：

においては，検定統計はHotellingTSquareDistribution[p,n-1]に従う：

母分散が既知である場合には，より強力なZTestを使うことができる：

ZTestはTTestよりも頻繁に を正しく退ける：

TTestは正規性からの少しの偏差に対して強固である：

値はそれでも通常通りに解釈することができる：

正規性からの大きい偏差には，中央値に基づく検定を使う必要がある：

値は，SignedRankTestについては通常通りに解釈することができるが，TTestについてはできない：

正規性のないデータの2つのサンプルの検定にはMannWhitneyTestを使う：

正規性のないデータにはMannWhitneyTestの方がTTestよりも強力であることがある：

TTestは，入力がTimeSeriesのときにのみ値に使うことができる：

TTestは，入力がTemporalDataのときはすべての値に使うことができる：

すべての値のみを検定する：

2つの経路の平均が等しいかどうかの検定を行う：

考えられる問題  (2)

TTestは，データが正規分布に従うと仮定する：

正規性を仮定しない中央値に基づく検定を使う：

多変量データの共分散行列は可逆ではないことがある：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), TTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/TTest.html.

テキスト

Wolfram Research (2010), TTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/TTest.html.

CMS

Wolfram Language. 2010. "TTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TTest.html.

APA

Wolfram Language. (2010). TTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TTest.html

BibTeX

@misc{reference.wolfram_2024_ttest, author="Wolfram Research", title="{TTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/TTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ttest, organization={Wolfram Research}, title={TTest}, year={2010}, url={https://reference.wolfram.com/language/ref/TTest.html}, note=[Accessed: 22-November-2024 ]}