WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

ToNumberField

ToNumberField[a,θ]

θ によって生成される数体で代数的数 a を表現する．

ToNumberField[{a₁,a₂,…},θ]

θ によって生成される体で a_iを表現する．

ToNumberField[{a₁,a₂,…}]

1つの代数的数が生成する共通の拡大体で a_iを表現する．

詳細

ToNumberFieldは，有限拡大体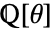の元に対応するAlgebraicNumberオブジェクトを与える．
ToNumberField[a,θ]は，a が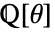に存在しない場合は未評価のまま残される．
a_iと θ はRootオブジェクトおよびAlgebraicNumberオブジェクトによって，あるいは通常の有理数と根基によって与えられる．
θ が代数的整数の場合，結果は常にAlgebraicNumber[θ,list]によって与えられる．
ToNumberField[{a₁,a₂,…}]は，a_iの表現を体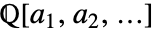の原始元によって与える．
ToNumberField[{a₁,a₂,…}]はToNumberField[{a₁,a₂,…},Automatic]に等しく，最小共通拡大体を使うとは限らない．
ToNumberField[{a₁,a₂,…},All]は常に最小共通拡大体を使う．
ToNumberField[x]は任意の形の代数的数を明示的なAlgebraicNumberオブジェクトに変換する．

例題

すべて開くすべて閉じる

例 (1)

をが生成する数体で表現する：

スコープ (6)

数体の生成元 θ は代数的整数に自動的に簡約される：

無理式：

Rootオブジェクト：

AlgebraicNumberオブジェクト：

とを共通の拡大体で表す：

代数的数を最小共通拡大体で表す：

アプリケーション (1)

上での原始元を求める：

特性と関係 (1)

代数的数を明示的なAlgebraicNumberオブジェクトに変換する：

トップへ