Extension

Extension

is an option for various polynomial and algebraic functions that specifies generators for the algebraic number field to be used.

Details

  • For polynomial functions, Extension determines the algebraic number field in which the coefficients are assumed to lie.
  • The setting Extension->a specifies the field 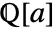consisting of the rationals extended by the algebraic number a.
  • Extension->{a1,a2,…} specifies the field .
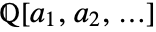  • The ai must be exact numbers, and can involve radicals as well as Root and AlgebraicNumber objects.
  • Extension->Automatic specifies that any algebraic numbers that appear in the input should be included in the extension field.
  • For polynomial functions, the default setting Extension->None specifies that all coefficients are required to be rational. Any algebraic numbers appearing in input are treated like independent variables.
  • Extension->{a1,a2,…} includes both the ai and any algebraic numbers in the input.
  • GaussianIntegers->True is equivalent to Extension->I.

Examples

open allclose all

Basic Examples  (2)

Factor a polynomial over :

PolynomialGCD over the field generated by the algebraic numbers present in the coefficients:

Scope  (8)

By default, factorization is performed over the rationals:

This specifies the factorization should be done over the rationals extended by :

Here the factorization is done over the rationals extended by and I:

By default, PolynomialGCD treats algebraic numbers as independent variables:

This computes the GCD over the algebraic number field generated by the coefficients:

By default, Together treats algebraic numbers as independent variables:

With Extension->Automatic, Together recognizes algebraically dependent coefficients:

By default, the norm is computed in the field generated by the AlgebraicNumber object:

This computes the norm in the field in which the AlgebraicNumber object is represented:

This computes the norm in the field generated by :

Properties & Relations  (1)

For Factor, Extension->I is equivalent to GaussianIntegers->True:

Wolfram Research (1996), Extension, Wolfram Language function, https://reference.wolfram.com/language/ref/Extension.html (updated 2007).

Text

Wolfram Research (1996), Extension, Wolfram Language function, https://reference.wolfram.com/language/ref/Extension.html (updated 2007).

CMS

Wolfram Language. 1996. "Extension." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Extension.html.

APA

Wolfram Language. (1996). Extension. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Extension.html

BibTeX

@misc{reference.wolfram_2024_extension, author="Wolfram Research", title="{Extension}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Extension.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_extension, organization={Wolfram Research}, title={Extension}, year={2007}, url={https://reference.wolfram.com/language/ref/Extension.html}, note=[Accessed: 22-December-2024 ]}