TransferFunctionCancel
相消 TransferFunctionModel tfm 中的共极点和零点.
TransferFunctionCancel[tfm,crit]
只相消 crit[ei] 为 True 的共极点-零点对 ei.
更多信息和选项
- 使用 TransferFunctionPoles 和 TransferFunctionZeros 计算极点和零点.
- TransferFunctionCancel 接受选项 Tolerance.
- 设置 Tolerance->ϵ,满足
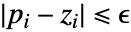 的极点
的极点 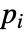 和零点
和零点 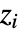 相消.
相消.
范例
打开所有单元关闭所有单元范围 (7)
应用 (1)
使用 TransferFunctionCancel 获得与陷波滤波器级联的高振荡系统的更简单表示:
属性和关系 (1)
对于 SISO 系统, TransferFunctionCancel 等同于 MinimalStateSpaceModel:
可能存在的问题 (2)
Wolfram Research (2010),TransferFunctionCancel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TransferFunctionCancel.html.
文本
Wolfram Research (2010),TransferFunctionCancel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TransferFunctionCancel.html.
CMS
Wolfram 语言. 2010. "TransferFunctionCancel." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TransferFunctionCancel.html.
APA
Wolfram 语言. (2010). TransferFunctionCancel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TransferFunctionCancel.html 年