TriangulateMesh

TriangulateMesh[bmr]

メッシュ領域 mr の三角形分割を生成する．

詳細とオプション

  • TriangulateMeshは，三角分解，四面体分解，単体分解，メッシュ生成，メッシュ細分化としても知られている．
  • 一般に，何らかの基準で最適化された，領域の線分への分割(1D)，三角形への分割(2D)，あるいは四面体への分割(3D)の生成に使われる．
  • TriangulateMeshには，MeshRegionと同じオプションに以下の追加・変更を加えたものが使える．
  • MaxCellMeasure Automatic最大セル測度
    MeshQualityGoal Automaticメッシュセルの品質目標
    MeshRefinementFunction Noneメッシュセルの細分化が必要な場合にTrueを返す関数
    MethodAutomatic使用するメソッド
    PerformanceGoal$PerformanceGoalスピードまたは品質を考慮するかどうか
  • Methodオプションの可能な設定には以下がある．
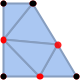
  • "ConformingDelaunay"ドロネー条件を満足する三角形分割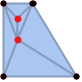
    "ConstrainedDelaunay"もとの1D境界セルを保持してドロネー条件をほぼ満足する三角形分割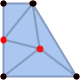
    "ConstrainedQuality"より少ない0Dセルを加えてドロネー条件をほぼ満足する三角形分割
  • メッシュ mr の三角形分割 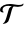は，mr の境界上にあるもとの点が 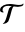の中の任意の単体の外接球内に一つもない場合はドロネー条件を満足する．

例題

すべて開くすべて閉じる

例  (3)

1DにおいてBoundaryMeshRegionを三角形分割する：

オプションを使ってセルの品質と大きさを制御する：

2DにおいてBoundaryMeshRegionを三角形分割する：

オプションを使ってセルの品質と大きさを制御する：

3DにおいてBoundaryMeshRegionを三角形分割する：

オプションを使ってセルの品質と大きさを制御する：

スコープ  (4)

1DにおけるBoundaryMeshRegionの三角形分割：

2Dにおける三角形分割：

3Dにおける三角形分割：

1DにおけるMeshRegionの三角形分割：

2Dにおける三角形分割：

3Dにおける三角形分割：

TriangulateMeshは次元の成分に個別に作用する：

MaxCellMeasureは，三角形分割におけるセルの可能な最大サイズを制御する：

使用される測度は，1Dメッシュでは弧長，2Dメッシュでは面積，3Dメッシュでは体積である：

オプション  (28)

MaxCellMeasure  (6)

1D領域で，さまざまな長さの制約を設ける：

2D領域で，さまざまな面積の制約を設ける：

さまざまな三角形の面積：

2D領域に辺の長さの制約を設ける：

さまざまな辺の長さ：

3D領域に体積の制約を設ける：

さまざまな四面体の体積：

3D領域に面の面積の制約を設ける：

さまざまな面の面積：

3D領域に辺の長さの制約を設ける：

さまざまな辺の長さ：

MeshCellHighlight  (3)

MeshCellHighlightを使ってTriangulateMeshの一部のハイライトを指定することができる：

面を透過的にすることで，3DのMeshRegionの内部構造を見ることができる：

個々のセルはセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

MeshCellLabel  (3)

MeshCellLabelを使ってTriangulateMeshの一部にラベルを付けることができる：

多角形の頂点と辺にラベルを付ける：

個々のセルにはセル指標を使ってラベルを付けることができる：

セルそれ自体を使うこともできる：

MeshCellMarker  (1)

MeshCellMarkerを使ってTriangulateMeshの一部に値を割り当てることができる：

MeshCellLabelを使ってマーカーを示す：

MeshCellShapeFunction  (2)

MeshCellShapeFunctionを使ってTriangulateMeshの一部のための関数を指定することができる：

個々のセルはセル指標を使って描くことができる：

セルそれ自体を使うこともできる：

MeshCellStyle  (3)

MeshCellStyleを使ってTriangulateMeshの一部のスタイルを指定することができる：

面を透過的にすることで，3DのMeshRegionの内部構造を見ることができる：

個々のセルはセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

MeshQualityGoal  (4)

デフォルト設定はAutomaticである：

"Minimal"品質の三角形分割を生成する：

"Maximal"品質の三角形分割を生成する：

明示的に数量的品質目標を定める：

MeshRefinementFunction  (4)

MeshRefinementFunctionを使って原点の左の辺を短くする：

MeshRefinementFunctionを使って第1象限の三角形を小さくする：

連続的に変化する面積についての制限を設定する：

第1象限を，より細かく離散化する：

PlotTheme  (2)

格子線と凡例のあるテーマを使う：

テーマを使ってワイヤーフレームを描く：

アプリケーション  (4)

多角形を三角形分割する：

最少の三角形分割：

基本的な3Dプリミティブを三角形分割する：

最少の三角形分割：

モナコの境界線の内側を三角形分割する：

三角形の数を最少にして分割する：

最大面積が最高でになるように三角形分割する：

領域の非線形変換は，頂点を変換することで近似することができる：

メッシュ内にはほとんど点がないので，変換ではうまく近似できない：

三角形分割を行うことで，より正確な近似が得られることがある：

特性と関係  (2)

TriangulateMeshの出力は，常にMeshRegionである：

TriangulateMeshの出力中のセルは，常に単体である：

2Dでは，単体は三角形である：

Wolfram Research (2014), TriangulateMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/TriangulateMesh.html （2020年に更新）.

テキスト

Wolfram Research (2014), TriangulateMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/TriangulateMesh.html （2020年に更新）.

CMS

Wolfram Language. 2014. "TriangulateMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/TriangulateMesh.html.

APA

Wolfram Language. (2014). TriangulateMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangulateMesh.html

BibTeX

@misc{reference.wolfram_2024_triangulatemesh, author="Wolfram Research", title="{TriangulateMesh}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/TriangulateMesh.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_triangulatemesh, organization={Wolfram Research}, title={TriangulateMesh}, year={2020}, url={https://reference.wolfram.com/language/ref/TriangulateMesh.html}, note=[Accessed: 22-November-2024 ]}