UnilateralDiscreteConvolve

UnilateralDiscreteConvolve[f,g,k,n]

gives the unilateral discrete convolution with respect to k of the expressions f and g.

UnilateralDiscreteConvolve[f,g,{k1,…,kp},{n1,…,np}]

gives the multidimensional unilateral discrete convolution.

Details and Options

  • UnilateralDiscreteConvolve is also known as causal convolution.
  • Unilateral convolution arises naturally when examining causal systems. The output of such systems at any time depends only on values of the input at the present time and in the past.
  • The unilateral convolution 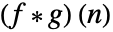of two sequences 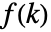and 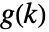is given by .
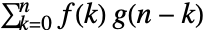  • The multidimensional convolution is given by .
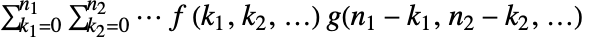  • The following options can be given:
  • Assumptions$Assumptionsassumptions to make about parameters
    GenerateConditionsFalsewhether to generate conditions on parameters
    MethodAutomaticmethod to use

Examples

open allclose all

Basic Examples  (4)

Convolve a sequence with DiscreteDelta:

Convolve a pair of step sequences:

Plot the result:

Convolve a linear sequence and a harmonic sequence and plot the result:

Unilateral convolution of multivariate sequences:

Scope  (6)

Convolve sequences of binomial coefficients:

Convolution of polynomial sequences:

Convolution of exponential sequences:

Plot the result:

Convolution of trigonometric sequences:

Plot the result:

Multivariate convolution with DiscreteDelta:

Multivariate convolution of rational sequences:

Applications  (2)

Obtain a particular solution for a linear ordinary difference equation using convolution:

Find the product of two power series:

Verify the result using Sum:

Properties & Relations  (8)

UnilateralDiscreteConvolve computes a sum over a finite interval:

Convolution with DiscreteDelta gives the function itself:

Scaling:

Commutativity:

Distributivity:

DiscreteConvolve coincides with UnilateralDiscreteConvolve for causal sequences:

The Z transform of a causal convolution is a product of the individual transforms:

Verify the convolution theorem for Z transforms on the following example:

The generating function of a causal convolution is a product of the individual generating functions:

Verify the convolution theorem for generating functions on the following example:

Wolfram Research (2024), UnilateralDiscreteConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html.

Text

Wolfram Research (2024), UnilateralDiscreteConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html.

CMS

Wolfram Language. 2024. "UnilateralDiscreteConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html.

APA

Wolfram Language. (2024). UnilateralDiscreteConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html

BibTeX

@misc{reference.wolfram_2024_unilateraldiscreteconvolve, author="Wolfram Research", title="{UnilateralDiscreteConvolve}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unilateraldiscreteconvolve, organization={Wolfram Research}, title={UnilateralDiscreteConvolve}, year={2024}, url={https://reference.wolfram.com/language/ref/UnilateralDiscreteConvolve.html}, note=[Accessed: 22-December-2024 ]}