Upsample

Upsample[array,n]

returns an upsampled version of the array by inserting zeros between array elements.

Upsample[array,n,offset]

shifts array so that its first element moves to the position offset in the resulting array.

Upsample[array,n,offset,val]

inserts elements of value val between array elements.

Upsample[image,…]

upsamples an image.

Details

  • In Upsample[array,…], array can be an array of any rank.
  • Upsample works with arrays of any rank and 2D and 3D images.
  • Upsample[array,{n1,n2,…}] inserts ni zeros between elements in the i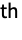^(th) dimension.
  • Upsample[array,n] is equivalent to Upsample[array,n,1].
  • In Upsample[array,n,offset], the offset has to be an integer between 1 and n.

Examples

open allclose all

Basic Examples  (3)

Upsample a list by a factor of 3:

Use an offset:

Specify the value to be inserted:

Upsample a 2D array:

Upsample an image by a factor of 2:

Scope  (3)

Use a different upsampling factor in each dimension:

Upsample a symbolic array:

Upsample an image by a factor of 2:

By default, using offset equal to 1, no shifting is performed:

Use a larger offset:

Use a different offset in each dimension:

Specify the insertion value:

Applications  (3)

Create a Nyquist filter of length 7:

Upsample by a factor of 2 using the smoothing filter:

Linear interpolation using upsampling and convolution:

This implementation is not very efficient:

A faster implementation would merge convolutions of the signal with odd and even samples of the filter:

Linear interpolation by a factor :

Wolfram Research (2012), Upsample, Wolfram Language function, https://reference.wolfram.com/language/ref/Upsample.html (updated 2016).

Text

Wolfram Research (2012), Upsample, Wolfram Language function, https://reference.wolfram.com/language/ref/Upsample.html (updated 2016).

CMS

Wolfram Language. 2012. "Upsample." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Upsample.html.

APA

Wolfram Language. (2012). Upsample. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Upsample.html

BibTeX

@misc{reference.wolfram_2025_upsample, author="Wolfram Research", title="{Upsample}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/Upsample.html}", note=[Accessed: 08-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_upsample, organization={Wolfram Research}, title={Upsample}, year={2016}, url={https://reference.wolfram.com/language/ref/Upsample.html}, note=[Accessed: 08-May-2025 ]}