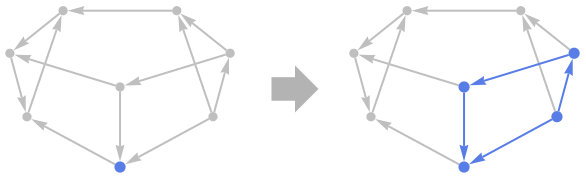
VertexInComponentGraph

VertexInComponentGraph[g,{v1,v2,…}]

gives the subgraph of the graph g generated by the vertices that have a directed path to at least one of v1,v2,….

VertexInComponentGraph[g,{v1,v2,…},k]

gives the subgraph of g generated by vertices with a directed path of at most length k to at least one of v1,v2,….

VertexInComponentGraph[g,{v1,v2,…},{k}]

gives the subgraph of g generated by vertices of length exactly k.

VertexInComponentGraph[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

Examples

open allclose all

Basic Examples  (3)

Find the in-component graph of a vertex:

Highlight the in-component graph of a vertex:

Find the in-component graph of a set of vertices in a graph:

Highlight the in-component graph of a vertex:

Scope  (9)

VertexInComponentGraph works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Tagged graphs:

Use rules to specify the graph:

Use patterns to select a subset of vertices:

Find the in-component graph connected to a vertex by a path of at most length 2 in a graph:

VertexInComponentGraph works with large graphs:

Applications  (2)

Find the message generating the largest total number of messages in the network of email sent to the MathGroup list in November 2011:

The most interesting subject of the month:

Show the network generated by this message:

Build a graph by states that can reach to state 4 within a finite step in a finite-state Markov chain with the following transition probability matrix:

Construct the state transition diagram of a transition matrix:

Build the graph by states that can reach to state 4:

Properties & Relations  (1)

Use VertexInComponent to find the in-component graph:

Wolfram Research (2021), VertexInComponentGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

Text

Wolfram Research (2021), VertexInComponentGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

CMS

Wolfram Language. 2021. "VertexInComponentGraph." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

APA

Wolfram Language. (2021). VertexInComponentGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VertexInComponentGraph.html

BibTeX

@misc{reference.wolfram_2024_vertexincomponentgraph, author="Wolfram Research", title="{VertexInComponentGraph}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/VertexInComponentGraph.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vertexincomponentgraph, organization={Wolfram Research}, title={VertexInComponentGraph}, year={2021}, url={https://reference.wolfram.com/language/ref/VertexInComponentGraph.html}, note=[Accessed: 21-December-2024 ]}