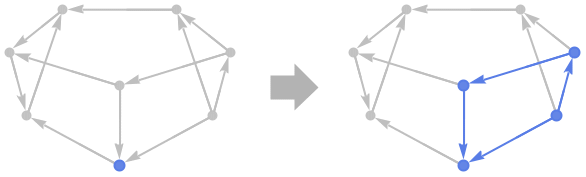
VertexInComponentGraph

VertexInComponentGraph[g,{v1,v2,…}]

给出图 g 的子图，该子图由具有到 v1,v2,… 中至少一个的有向路径的顶点生成.

VertexInComponentGraph[g,{v1,v2,…},k]

给出图 g 的子图，该子图由具有到 v1,v2,… 中至少一个、长度最多为 k 的有向路径的顶点生成.

VertexInComponentGraph[g,{v1,v2,…},{k}]

给出图 g 的子图，该子图由长度正好为 k 的顶点生成.

VertexInComponentGraph[{vw,…},…]

使用规则 vw 指定图 g.

更多信息和选项

范例

打开所有单元关闭所有单元

基本范例  (3)

求顶点的入分量子图：

突出显示顶点的入分量子图：

求图中一组顶点的入分量子图：

突出显示顶点的入分量子图：

范围  (9)

VertexInComponentGraph 适用于无向图：

有向图：

多图：

混合图：

已标注的图：

用规则指定图：

用模式选定顶点的子集：

求图中最多通过长度为 2 的路径连接到顶点的入分量子图：

VertexInComponentGraph 适用于大图：

应用  (2)

在 2011 年 11 月发送到 MathGroup 列表的电子邮件网络中查找生成最大邮件总数的邮件：

该月最有趣的主题：

显示此消息生成的网络：

用具有以下转移概率矩阵的有限状态马尔可夫链中的在有限步骤内可以到达状态 4 的状态来构建图：

构建转移矩阵的状态转移图：

用可以达到状态 4 的状态来构建图：

属性和关系  (1)

用 VertexInComponent 求入分量子图：

Wolfram Research (2021)，VertexInComponentGraph，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

文本

Wolfram Research (2021)，VertexInComponentGraph，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

CMS

Wolfram 语言. 2021. "VertexInComponentGraph." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/VertexInComponentGraph.html.

APA

Wolfram 语言. (2021). VertexInComponentGraph. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VertexInComponentGraph.html 年

BibTeX

@misc{reference.wolfram_2024_vertexincomponentgraph, author="Wolfram Research", title="{VertexInComponentGraph}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/VertexInComponentGraph.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vertexincomponentgraph, organization={Wolfram Research}, title={VertexInComponentGraph}, year={2021}, url={https://reference.wolfram.com/language/ref/VertexInComponentGraph.html}, note=[Accessed: 18-November-2024 ]}