WaveletScale
is an option for ContinuousWaveletTransform and related constructs used to specify the smallest resolvable scale.
Details
- WaveletScale
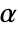represents the smallest resolvable scale in a ContinuousWaveletTransform. - The continuous wavelet transform of a uniformly sampled sequence
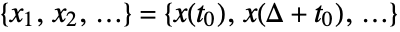is given by )/s)](Files/WaveletScale.en/3.png "w(u,s)=1/(sqrt(s))sum_(k=1)^nx_k TemplateBox[{psi}, Conjugate]((Delta (k-u))/s)")
. - The scaling parameter
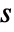is given by equal-tempered scale 
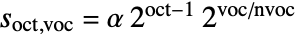where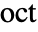 
is the octave number, 
the voice number, and 
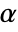the smallest wavelet scale. - The default value for WaveletScale
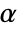is Automatic. The value of 
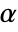can be any number greater than 0.
Examples
open allclose allBasic Examples (1)
WaveletScale indicates the smallest resolvable scale used for the transform:
The scales used are given as 
with 
wavelet scale, 
octave, and 
voice:
Properties & Relations (1)
Automatic value of WaveletScale is computed as the inverse of Fourier wavelet length of the wavelet:
GaborWavelet[w]:
DGaussianWavelet[n]:
PaulWavelet[n]:
Text
Wolfram Research (2010), WaveletScale, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletScale.html.
CMS
Wolfram Language. 2010. "WaveletScale." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletScale.html.
APA
Wolfram Language. (2010). WaveletScale. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletScale.html