WignerD

WignerD[{j,m1,m2},ψ,θ,ϕ]

WignerのD関数 を与える．

WignerD[{j,m1,m2},θ,ϕ]

WignerのD関数 を与える．

WignerD[{j,m1,m2},θ]

WignerのD関数 を与える．

詳細

  • WignerのD関数 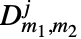は，パラメータ 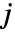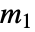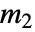，， が物理的であるとき，すなわちすべてが 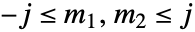であるような整数か半整数であるときに，回転群の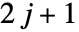次元のユニタリ表現におけるオイラー(Euler)角によってパラメータ化された回転演算子の行列要素を与える．
  • 非物理的なパラメータについては，WignerDは解析接続によって定義される．
  • Wolfram言語は TemplateBox[{j, {m, _, 1}, {m, _, 2}, psi, theta, phi}, WignerD]=exp(ⅈ m_1 psi+ⅈ m_2phi) TemplateBox[{j, {m, _, 1}, {m, _, 2}, 0, theta, 0}, WignerD]であるところでは位相規則を使う．

例題

すべて開くすべて閉じる

例  (1)

整数値の物理パラメータで評価する：

半整数の物理パラメータで評価する：

スコープ  (1)

物理的パラメータについて数値的に評価する：

一般化と拡張  (1)

非物理的パラメータについて数値的に評価する：

アプリケーション  (1)

1/2スピン表現について回転行列を構築する：

ユニタリ性をチェックする：

スピノルから3Dベクトルを構築する：

スピノル基底は座標基底に平行移動される：

スピノルのユニタリ変換に誘導された座標変換：

結果の回転行列をオイラー角から直接構築する：

特性と関係  (4)

消失パラメータ m1については，WignerDはSphericalHarmonicYに変換される：

Wigner D行列の行列要素はある種の対称関係を満たす：

群の直交基底からのWignerD関数：

積分は2/(2 j_1+1) (4 pi)^2TemplateBox[{{{j, _, 1}, ,, {j, _, 2}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 11, )}}, ,, {m, _, {(, 21, )}}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 12, )}}, ,, {m, _, {(, 22, )}}}}, KroneckerDeltaSeq]と等値である：

2つのWignerD関数の積はClebschGordan係数を使ったWignerD関数によって表すことができる：

Wolfram Research (2010), WignerD, Wolfram言語関数， https://reference.wolfram.com/language/ref/WignerD.html.

テキスト

Wolfram Research (2010), WignerD, Wolfram言語関数， https://reference.wolfram.com/language/ref/WignerD.html.

CMS

Wolfram Language. 2010. "WignerD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WignerD.html.

APA

Wolfram Language. (2010). WignerD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WignerD.html

BibTeX

@misc{reference.wolfram_2024_wignerd, author="Wolfram Research", title="{WignerD}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WignerD.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_wignerd, organization={Wolfram Research}, title={WignerD}, year={2010}, url={https://reference.wolfram.com/language/ref/WignerD.html}, note=[Accessed: 18-November-2024 ]}