"AVLTree" （数据结构）

"AVLTree"

表示一个可变的、自平衡的二叉搜索树，其中存储在每个节点上的值为普通表达式.

更多信息

  • 二进制搜索树以允许进行快速插入操作的排序形式存储数据. 自平衡二进制搜索树可确保所有分支的高度是平衡的；这使得无论是进行插入和删除，都非常高效.
  • CreateDataStructure[ "AVLTree"]创建一个空的 "AVLTree"
    CreateDataStructure["AVLTree",v{l,r}]创建具有指定初始值 v 和指定左子树和右子树的新的 "AVLTree"
    CreateDataStructure["AVLTree",tree,p]使用指定树和排序函数 p 创建新的 "AVLTree
    Typed[x,"AVLTree"]指定 x 的类型为 "AVLTree"
  • 对于类型为 "AVLTree" 的数据结构，可进行以下操作：
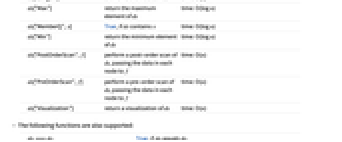
  • ds["BreadthFirstScan",f]对 ds 执行广度优先扫描，将每个节点的数据传递给 f用时：O(n)
    ds["Copy"]返回 ds 的副本用时：O(n)
    ds["Delete",x]从 ds 中删除 x用时：O(log n)
    ds["DeleteAll"]删除 ds 中所有的元素用时：O(n)
    ds["DropMax"]移除 ds 的最大元素并将其返回用时：O(log n)
    ds["DropMin"]移除 ds 的最小元素并将其返回用时：O(log n)
    ds["Elements"]返回 ds 的元素列表用时：O(n)
    ds["EmptyQ"]如果 ds 没有节点则为 True用时：O(1)
    ds["FreeQ",x]如果 ds 不含有 x 则为 True用时：O(log n)
    ds["InOrderScan",f]对 ds 执行中序扫描，将每个节点的数据传递给 f用时：O(n)
    ds["Insert",x]将 x 插入 ds用时：O(log n)
    ds["Length"]ds 中节点的数量用时：O(1)
    ds["Max"]返回 ds 的最大元素用时：O(log n)
    ds["MemberQ",x]如果 ds 含有 x 则为 True用时：O(log n)
    ds["Min"]返回 ds 的最小元素用时：O(log n)
    ds["PostOrderScan",f]对 ds 执行后序扫描，将每个节点的数据传递给 f用时：O(n)
    ds["PreOrderScan",f]对 ds 执行前序扫描，将每个节点的数据传递给 f用时：O(n)
    ds["Visualization"]返回 ds 的可视化用时：O(n)
  • 还支持以下函数：
  • dsi===dsj如果 dsi 等于 dsj 则为 True
    FullForm[ds]ds 的完全形式
    Information[ds]关于 ds 的信息
    InputForm[ds]ds 的输入形式
    Normal[ds]将 ds 转换成普通表达式
  • Sort 排序函数给出结果后，两个元素的顺序由排序函数 p 决定. 默认的排序函数为 Order.
  • "AVLTree" 保持平衡的属性，即每个子树的高度相差不超过 1.
  • 若树的初始指定为 Null，则会创建一个空的 "AVLTree".

范例

打开所有单元关闭所有单元

基本范例  (1)

可用 CreateDataStructure 创建新的 "AVLTree"：

插入几个数值：

可视化数据结构：

范围  (4)

信息  (1)

可用 CreateDataStructure 创建新的 "AVLTree"：

数据结构 ds 的信息：

平衡  (1)

"AVLTree" 保持平衡，即每个子树的高度相差不超过 1：

可能破坏平衡属性的修改会导致重新进行平衡：

现在，右侧的插入不需要重新平衡：

从左侧删除则需要重新平衡：

排序  (1)

创建一棵新树并插入 30 个随机数：

下面对树进行中序扫描. 由于树已排序，因此按排好的顺序访问元素，如本例所示：

排序函数  (1)

使用自定义排序函数创建一颗空树：

插入数据：

树中的元素：

移除并返回最大的元素：

最大的元素已被移除：