"DynamicArray" (Data Structure)

"DynamicArray"

represents a dynamically extensible array where the elements are general expressions.

Details

  • An extensible array is useful for continuously appending elements, as well as for efficient element extraction and updating.
  • CreateDataStructure[ "DynamicArray"]create a new empty "DynamicArray"
    CreateDataStructure[ "DynamicArray",elems]create a new "DynamicArray" containing elems
    Typed[x,"DynamicArray"]give x the type "DynamicArray"
  • For a data structure of type "DynamicArray", the following operations can be used:
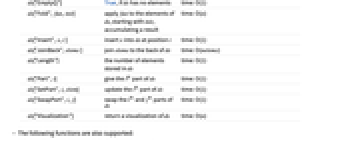
  • ds["Append",x]append x to dstime: O(1)
    ds["Copy"]return a copy of dstime: O(n)
    ds["Drop",i]drop the i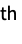^(th) part of dstime: O(n)
    ds["DropAll"]drop all the elements from dstime: O(n)
    ds["DropLast"]drop the last element of dstime: O(1)
    ds["Elements"]return a list of the elements of dstime: O(n)
    ds["EmptyQ"]True, if ds has no elementstime: O(1)
    ds["Fold",fun,init]apply fun to the elements of ds, starting with init, accumulating a resulttime: O(n)
    ds["Insert",x,i ]insert x into ds at position itime: O(1)
    ds["JoinBack",elems ]join elems to the back of dstime: O(nelems)
    ds["Length"]the number of elements stored in dstime: O(1)
    ds["Part",i]give the i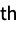^(th) part of dstime: O(1)
    ds["SetPart",i,elem]update the i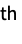^(th) part of dstime: O(1)
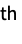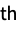    ds["SwapPart",i,j]swap the i^(th) and j^(th) parts of dstime: O(1)
    ds["Visualization"]return a visualization of dstime: O(n)
  • The following functions are also supported:
  • dsi===dsjTrue, if dsi equals dsj
    ds["Part",i]=valset i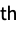^(th) element of ds to val
    FullForm[ds]full form of ds
    Information[ds]information about ds
    InputForm[ds]input form of ds
    Normal[ds]convert ds to a normal expression

Examples

open allclose all

Basic Examples  (2)

A new "DynamicArray" can be created with CreateDataStructure:

Elements can be appended:

Return the length:

Extract the first element:

Change an element:

The element has updated:

Return an expression version of ds:

It is fast to append:

A visualization of the data structure can be generated:

Sum all the elements:

Scope  (1)

Information  (1)

A new "DynamicArray" can be created with CreateDataStructure:

Information about the data structure ds:

Applications  (11)

Reverse  (1)

A simple function that carries out an in-place reverse of a "DynamicArray":

A sample data structure to use:

Reverse the elements:

Bubble Sort  (1)

Bubble sort is a simple sorting algorithm that is easy to code but typically has poor performance:

A sample data structure to use:

Sort the elements:

The data structure is sorted in place:

Insertion Sort  (1)

Insertion sort is a simple sorting algorithm that is easy to code and typically has poor performance for large arrays, but can be useful for small arrays:

A sample data structure to use:

Sort the elements:

The data structure is sorted in place:

Quicksort  (1)

Quicksort is an efficient sorting algorithm. This basic implementation uses nested functions:

A sample data structure to use:

Sort the elements:

The data structure is sorted in place:

Merge Sort  (1)

Merge sort is an efficient sorting algorithm. This is a simple implementation that uses a workspace:

A sample data structure to use:

Sort the elements:

The data structure is sorted in place:

Heapsort  (1)

Heapsort is an efficient sorting algorithm that works in place by constructing a heap:

A sample data structure to use:

The elements are sorted in place:

Timsort  (1)

Timsort is a hybrid and efficient sorting algorithm:

A sample data structure to use:

The elements are sorted in place:

Fisher–Yates Shuffle  (1)

The Fisher–Yates shuffle generates a random permutation of a finite sequence:

A sample array to use for the shuffle:

Apply the shuffle:

Palindrome  (1)

An array is a palindrome if it is symmetric around the middle:

This is not a palindrome:

This is a palindrome:

Quickselect  (1)

Quickselect is a selection algorithm related to the Quicksort algorithm. It returns the k^(th) smallest element in a list:

A sample data structure to use:

The third smallest element is 7:

Heap  (1)

A heap is a tree-based data structure where the value stored at children is smaller than that stored in their parents (for a min heap). It is commonly used to implement a priority queue and typically implemented with an array rather than a tree.

The following converts an array into a heap:

A sample data structure to use:

This converts the array into a heap; it is hard to see the heap property:

This function generates a tree:

A visualization makes it easier to see the min heap property:

Properties & Relations  (1)

"FixedArray"  (1)

Many algorithms that work for "DynamicArray" also work for "FixedArray".