"PriorityQueue" (データ構造)

"PriorityQueue"

優先度の最も高い要素が常に返される，要素のキューを表す．

詳細

  • 優先度付きキューは，効率的な挿入と削除の演算を行う．
  • CreateDataStructure["PriorityQueue"]新しい空の"PriorityQueue"を作成する
    CreateDataStructure["PriorityQueue",elems]要素 elems を持つ新しい"PriorityQueue"を作成する
    CreateDataStructure["PriorityQueue",elems,p]指定の要素と順序関数 p を持つ新しい"PriorityQueue"を作成する
    Typed[x,"PriorityQueue"]x に"PriorityQueue"型を与える
  • "PriorityQueue"型のデータ構造には，以下の演算が使える．
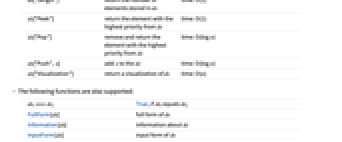
  • ds["Copy"]ds のコピーを返すtime: O(n)
    ds["DropAll"]ds からすべての要素を省くtime: O(n)
    ds["Elements"]ds の要素のリストを返すtime: O(n)
    ds["EmptyQ"]ds に要素が保存されていない場合はTrueを返すtime: O(1)
    ds["Length"]ds に保存される要素の数を返すtime: O(1)
    ds["Peek"]ds から優先度が最も高い要素を返すtime: O(1)
    ds["Pop"]ds から優先度が最も高い要素を削除して返すtime: O(log n)
    ds["Push",x]x を ds に加えるtime: O(log n)
    ds["Visualization"]ds の可視化を返すtime: O(n)
  • 以下の関数もサポートする．
  • dsi===dsjdsi が dsj に等しい場合はTrue
    FullForm[ds]ds の完全形
    Information[ds]ds についての情報
    InputForm[ds]ds の入力形
    Normal[ds]ds を通常の式に変換する
  • 2つの要素の順序は，Sortの順序関数によって与えられる解釈に従い，順序関数 p によって決定される．デフォルトの順序関数は，Orderである．
  • "PriorityQueue"は，ヒープデータ構造によって実装される．
  • 最初の要素の指定がNullである場合には，空の"PriorityQueue"が作成される．

例題

すべて開くすべて閉じる

例  (4)

新しい"PriorityQueue"は，CreateDataStructureを使って作成できる：

最初は何も要素が入っていない：

要素を3個挿入する：

優先度が最も高い要素を削除して返す：

任意データを"PriorityQueue"に保存することができる：

このデータ構造の可視化は，子よりも小さいノードがないというヒープ特性が維持されることを示す：

任意のデータを"PriorityQueue"に保存することができる：

要素のペアに関数を適用し，その順序を見極めることができる：

規則のリスト：

規則を追加してから優先度の高い規則を削除して返す．規則は，第1要素の優先度順に返される：

スコープ  (2)

ソート  (1)

ランダムなデータ：

"PriorityQueue"に挿入され，そこから削除されたデータは，逆のソート順に返される：

情報  (1)

新しい"PriorityQueue"は，CreateDataStructureを使って作成することができる：

データ構造 ds についての情報：

考えられる問題  (1)

ソート  (1)

優先度キューのデータ構造は，ヒープで実装される．これはつまり，要素が完全にソートされた順で維持されるわけではないことを意味する．要素の順序は，ヒープ特性だけを維持する．これは，部分的にしかソートされていない．

以下の挿入は，順序付けられた要素集合を返す：

以下の挿入は，順序付けられた要素集合を返さない：

要素を抽出すると，必ず順番に返される：

要素を抽出すると，必ず順番に返される：

完全にソートされた順を維持するバッファが必要な場合には，"AVLTree"等，別のデータ構造の方が好ましいこともある．