"Deque" (Data Structure)
"Deque"
represents a queue of expressions that can be added or removed from the front and back.
Details

- A deque is a collection of elements that supports both first-in, first-out and last-in, first-out insertion and removal:
-
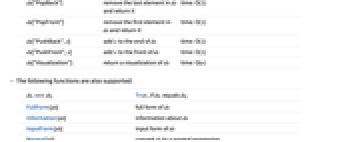
CreateDataStructure["Deque"] create a new empty "Deque" CreateDataStructure["Deque",elems] create a new "Deque" containing elems Typed[x,"Deque"] give x the type "Deque" - For a data structure of type "Deque", the following operations can be used:
-
ds["Copy"] return a copy of ds time: O(n) ds["DropAll"] drop all the elements from ds time: O(n) ds["Elements"] return a list of the elements of ds time: O(n) ds["EmptyQ"] True, if the ds is empty time: O(1) ds["Fold",fun,init] apply fun to the elements of ds, starting with init, accumulating a result time: O(n) ds["Length"] number of elements in ds time: O(1) ds["PeekBack"] the last element in ds time: O(1) ds["PeekFront"] the first element in ds time: O(1) ds["PopBack"] remove the last element in ds and return it time: O(1) ds["PopFront"] remove the first element in ds and return it time: O(1) ds["PushBack",x] add x to the end of ds time: O(1) ds["PushBackList",elems] add elems to the end of ds time: O(nelems) ds["PushFront",x] add x to the front of ds time: O(1) ds["PushFrontList",elems] add elems to the front of ds time: O(nelems) ds["Visualization"] return a visualization of ds time: O(n) - The following functions are also supported:
-
dsi===dsj True, if dsi equals dsj FullForm[ds] full form of ds Information[ds] information about ds InputForm[ds] input form of ds Normal[ds] convert ds to a normal expression
Examples
open all close allBasic Examples (2)
A new "Deque" can be created with CreateDataStructure:
Add another element and peek. This shows the first element:
Remove the last element and return it:
Return an expression version of ds:
It is fast to put elements into a queue:
Scope (1)
Information (1)
A new "Deque" can be created with CreateDataStructure:
Applications (1)
Minimum of a Partially Ordered Set (1)
A "Deque" is useful for computing the minimum of a partially ordered set. A partially ordered set needs an ordering function that can return Indeterminate if the elements do not have an ordering relation.
This returns the minimum of a set for the ordering function or Indeterminate if there is no minimum value:
This ordering function uses Divisible; if the numbers are not divisible by each other, the result is Indeterminate:
2 can be divided into both 4 and 6, so it is the minimum value:
There is no number here that can be divided into the others; the result is Indeterminate:
See Also
CreateDataStructure DataStructure
Data Structures: Queue RingBuffer DoublyLinkedList DynamicArray PriorityQueue
Related Guides
History
Introduced in 2020 (12.1)