WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"DBSCAN" (Machine Learning Method)

Details & Suboptions

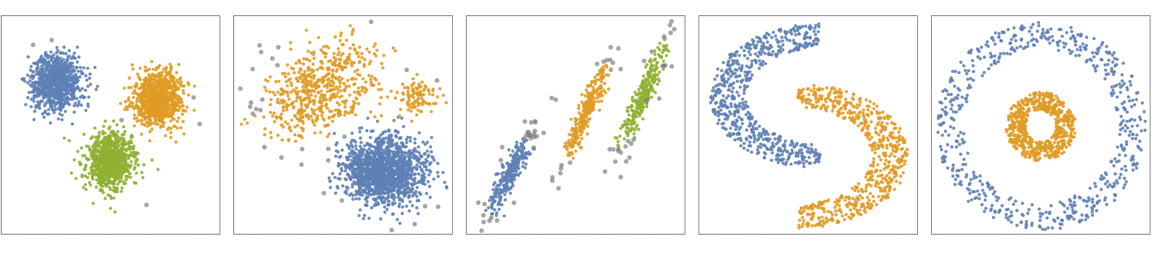
  • "DBSCAN" (density-based spatial clustering of applications with noise) is a density-based clustering method where the density is estimated using a neighbor-based approach. "DBSCAN" works for arbitrary cluster shapes and sizes but requires clusters to have similar densities.
  • The following plots show the results of the "DBSCAN" method applied to toy datasets (black points indicate outliers):
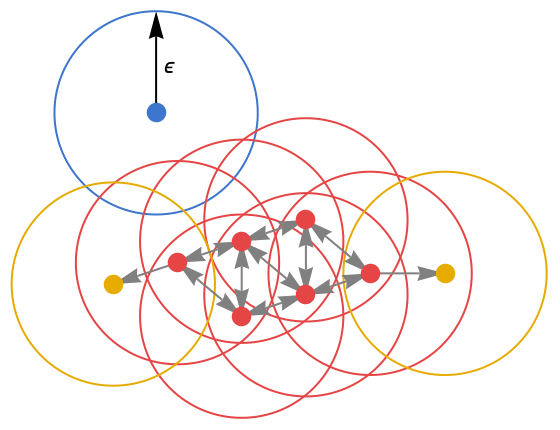
  • "DBSCAN" defines "core points" as data points that have more than k neighbors within a ball of ϵ radius (i.e. data points in high-density regions). Then, core points that are at a distance of less than ϵ from each other define a cluster. Furthermore, any point that is at a distance of less than ϵ of a core point belongs to the cluster of the core point. Any point that is not near a core point is considered noise.
  • This results in each cluster containing one or more core points at its core and some non-core points at its "edge". Overall, "DBSCAN" defines clusters as connected high-density regions. In the following figure, core points are red, edge points are yellow and noise points are blue:
  • In ClusteringComponents and ClusterClassify, noise points are labeled Missing["Anomalous"].
  • In FindClusters, noise points are returned as a cluster.
  • The option DistanceFunction can be used to define which distance to use.
  • The following suboptions can be given:
  • "NeighborhoodRadius" Automatic
    		radius ϵ
    "NeighborsNumber" Automaticnumber of neighbors k
    "DropAnomalousValues" Falsewhether to drop outliers

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Find clusters of nearby values using the "DBSCAN" method:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-wxc5bs
Out[1]=1

Train the ClassifierFunction on a list of colors using the "DBSCAN" method:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-509fvf
Out[1]=1

Gather the elements by their class number:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-izazxv
Out[2]=2

Create random 2D vectors:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-q8s2rm
Out[1]=1

Plot clusters in data found using the "DBSCAN" method:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-fj7crm
Out[2]=2

Scope  (2)Survey of the scope of standard use cases

Obtain a random list of times:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-3sq4zb
Out[1]=1

Train the ClassifierFunction using the "DBSCAN" method:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-0wodlh
Out[2]=2

Obtain the cluster assignment and cluster the data:

In[3]:=3
✖
https://wolfram.com/xid/0bfevoay07hcec-s8b4j2
Out[3]=3
Out[3]=3

Train the ClassifierFunction using the "DBSCAN" method:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-g11jal
Out[1]=1

Noise points are labeled as Missing["Anomalous"]:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-5s1s23
Out[2]=2

Options  (7)Common values & functionality for each option

DistanceFunction  (1)

Cluster string data using edit distance:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-ozzii5
Out[1]=1

Cluster data using Manhattan distance:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-xbfrhk
Out[2]=2

"NeighborhoodRadius"  (2)

Find clusters by specifying the "NeighborhoodRadius" suboption:

In[7]:=7
✖
https://wolfram.com/xid/0bfevoay07hcec-3656v8
Out[7]=7

Define a set of two-dimensional data points, characterized by four somewhat nebulous clusters:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-0l2e30
Out[1]=1

Plot clusters in data found using the "DBSCAN" method:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-9b0lj5
Out[2]=2

Plot different clusterings of data using the "DBSCAN" method by varying the "NeighborhoodRadius":

In[3]:=3
✖
https://wolfram.com/xid/0bfevoay07hcec-z3ek06
Out[3]=3

"NeighborsNumber"  (3)

Find clusters by specifying the "NeighborsNumber" suboption:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-fip5bm
Out[1]=1

Create random 2D vectors:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-4onycb
Out[1]=1

Plot clusters in data found using the "DBSCAN" method:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-khjy3n
Out[2]=2

Plot different clusterings of data using the "DBSCAN" method by varying the "NeighborsNumber":

In[3]:=3
✖
https://wolfram.com/xid/0bfevoay07hcec-iauvn5
Out[3]=3

Define a set of two-dimensional data points, characterized by four somewhat nebulous clusters:

In[1]:=1
✖
https://wolfram.com/xid/0bfevoay07hcec-tox9eg
Out[1]=1

Plot clusters in data using the "DBSCAN" method:

In[2]:=2
✖
https://wolfram.com/xid/0bfevoay07hcec-hxic61
Out[2]=2

Plot different clusterings of data using the "DBSCAN" method by varying the "NeighborsNumber":

In[3]:=3
✖
https://wolfram.com/xid/0bfevoay07hcec-ru8gw9
Out[3]=3

"DropAnomalousValues"  (1)

Train the ClassifierFunction, which labels outliers as Missing["Anomalous"]:

In[10]:=10
✖
https://wolfram.com/xid/0bfevoay07hcec-jhla3c
Out[11]=11

Use the trained ClassifierFunction to identify the outliers:

In[12]:=12
✖
https://wolfram.com/xid/0bfevoay07hcec-w4txzt
Out[12]=12

Train the ClassifierFunction by dropping outliers and finding new cluster assignments:

In[13]:=13
✖
https://wolfram.com/xid/0bfevoay07hcec-mn7l7q
Out[13]=13
Out[14]=14

Similarly, find clusters of nearby values with outliers:

In[18]:=18
✖
https://wolfram.com/xid/0bfevoay07hcec-5at6h4
Out[18]=18

Remove outliers using the "DropAnomalousValues" suboption:

In[17]:=17
✖
https://wolfram.com/xid/0bfevoay07hcec-ozd2vx
Out[17]=17