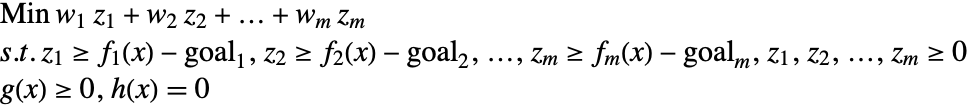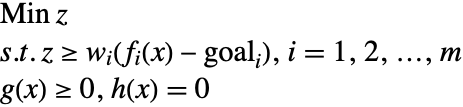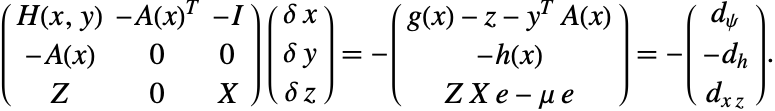局所的非線形数値最適化

はじめにFindMinimumの例題
FindMinimum関数制約条件付き局所的最適化の数値アルゴリズム

はじめに

制約条件付きの非線形最適化に対する数値アルゴリズムは，大まかに分けると勾配法と直接探索法とに分けられる．勾配法では，第1導関数（勾配）か第二導関数（ヘッシアン）の乗法が使われる．この例にはSQP(逐次二次計画)法，拡大ラグランジュ法，非線形内点法がある．直接探索法では，導関数情報は使われない．この例としては，Nelder-Mead法，遺伝的アルゴリズム，微分進化法，焼きなまし法がある．直接探索法の方が収束が遅い傾向があるが，関数と制約条件のノイズの存在への耐性は強い．

通常，アルゴリズムは問題の局所的なモデルを構築するだけである．また，そのようなアルゴリズムの多くは目的関数の減少，目的関数と制約条件の組み合わせであるメリット関数の減少を要求し，反復プロセスの収束を確実にする．収束した場合，このアルゴリズムは局所的最適値だけを見付けるため，「局所的最適化アルゴリズム」と呼ばれる．Wolfram言語では，局所的最適化問題はFindMinimumを使って解くことができる．

一方，大域的最適化アルゴリズムは，一般に目的・メリット関数の増加と減少を許可することにより，大域的最適値を見付けようとする．このアルゴリズムは通常計算的により高価である．大域的最適値問題は，Minimizeを使って厳密にとくことも，NMinimizeを使って数値的に解くこともできる．

下の非線形計画問題 をMinimizeで解く．厳密解が得られる
次に，同じ問題を数値的に解く．NMinimizeは機械数の解を返す：
FindMinimumは数値的に局所的最小値を見付ける．この例では，見付かった局所的最小値は，大域的最小値でもある：

FindMinimum関数

FindMinimumは，制約条件なしおよび制約条件付きの最適化問題を解く．ここでは制約条件付きの最適化だけを扱う．制約条件なしの最適化でのFindMinimumの詳細は，「制約条件のない最適化」を参照のこと．

下の非線形計画問題 をFindMinimumを使って解く：
以下でFindMinimumにxの初期値2を与え，yにはデフォルトの初期値を使う：

前の解の点は実際には局所的最小値である．FindMinimumは局所的最小値だけを見付ける．

下の実現可能領域の等高線プロットは，局所的および大域的最小値を示している：
実現可能領域の関数の3Dによる可視化である：

FindMinimumのオプション

FindMinimumは次のオプションを取ることができる．

オプション名
デフォルト値
AccuracyGoalAutomatic目標確度
CompiledAutomatic関数と制約条件を自動的にコンパイルするかどうか
EvaluationMonitorNonef が評価されるときに常に評価する式
GradientAutomatic勾配関数のリスト{D[f,x],D[f,y],…}
MaxIterationsAutomatic使用する最大反復回数
MethodAutomatic使用するメソッド
PrecisionGoalAutomatic目標精度
StepMonitorNoneステップが取られたときに常に評価する式
WorkingPrecisionMachinePrecision内部計算で使用される精度

FindMinimum関数のオプション

Methodオプションは，最適化問題を解くのに使用するメソッドを指定する．現在制約条件付き最適化に使用できる唯一のメソッドは内点法である．

これで内点法を使うよう指定する：

MaxIterationsオプションは使用する最大反復回数を指定する．制約条件付きの最適化に機械精度が使われるときは，デフォルトのMaxIterations->500が使われる．

StepMonitorが指定されると，内点法の各反復ステップで1度ずつ評価される．また，EvaluationMonitorが指定されると，同値制約または不同値制約の関数が評価されるたびに，これが評価される．

デフォルトの許容誤差まで下の問題を解くには，10回の反復では不十分である．StepMonitorを使って，訪れた点を集める：
訪れた点をContourPlotを使って示す．初期値は青で，その他は黄色で表示されている：

WorkingPrecision->prec は，FindMinimumの計算をすべて精度 prec で実行するよう指定する．デフォルトは precMachinePrecisionである．prec>MachinePrecisionならば，計算すべてで prec の固定精度が使われる．

AccuracyGoalオプションとPrecisionGoalオプションは，次のように使われる．デフォルトではAccuracyGoal->Automaticであり，prec/3に設定される．デフォルトはPrecisionGoal->Automaticであり，-Infinityに設定される．AccuracyGoal->ga はAccuracyGoal->{-Infinity,ga}と同じである．

AccuracyGoal->{a,ga}およびPrecisionGoal->p であるならば，FindMinimumは，実現可能性とKKT(Karush-Kuhn-Tucker) 条件の満足度と相補条件の組合せである残差を，tol=10-ga 以下にしようとする．また，FindMinimumでは現行と次の反復点 x と x+の差分が，終了前にを満足することが必要である．

WorkingPrecisionを100にして解を計算する：
厳密な最適値はMinimizeを使って計算され，FindMinimumの結果と比較される：

FindMinimumの例題

大域的最小値を見付ける

大域的最小値が必要な場合，NMinimizeかMinimizeを使わなければならない．しかし，FindMinimumの方がNMinimizeとMinimizeよりも速い傾向にあるので，極小値の少ない比較的大きい問題では特に，FindMinimumを使った方が効率的なことがある．FindMinimumは極小値を求めようとするので，極小値が見つかると終了する．

以下は，実行可能範囲-10≤x≤10内で複数の極小値を持つ関数を示している：
初期値が自動のときは，FindMinimumは極小値に収束する：
問題のことがよく分かっている場合は，FindMinimumにより適した初期値を与えることができる：
あるいは，制約条件を厳しくすることもできる：
また，複数の初期値を使い，最適な結果を選ぶこともできる：
NMinimizeで"RandomSearch"を使い，後処理に内点法で使うと，より体系的に複数の初期値を実行することができる：

Minimax問題を解く

minimax（minmaxとしても知られる）問題は，いくつかの関数の最大値として定義された関数の最小値を見付けるという問題である．つまり，以下のようなものである．

この問題は，一般の制約条件付き最適化手法を使って解くことができる場合が多いが，問題を滑らかな目的関数を持つ問題に再形式化することによりより簡単に解くことができる．特にminimax問題は次の形式

に変換し，FindMinimumかNMinimizeを使って解くことができる．

以下は関数FindMinMaxを定義する：
次で，制約条件のない1変数のminimax問題を解く：
これは，制約条件のない2変数のminimax問題を解く：
以下は目的関数の等高線と，最適解を示す：
次は制約条件付きのminimax問題を解く：
これは実現可能領域内の目的関数の等高線，およびその最適解を示す：

多目的最適化：目標計画法

多目的計画法には，制約条件を対象としていくつかの目的関数を最小化することが含まれる．1つの関数を最小化する解は通常他の関数を最小化することはあまりないので，一意の最適解は通常ない．

意思決定者は書く目的に対する目標を想定していることがある．その場合，いわゆる目標計画法を適用することができる．

目標計画法問題をモデル化する方法には多数の変形がある．そのひとつに，優先順位に基づいて目的関数を並べ，重要度の低い目的関数の目標からの偏差を最小化使用とする前に，最も重要な目的関数の目標からの偏差の最小化を求めるというものがある．これは辞書的あるいは先取り目標計画法と呼ばれる．

2つ目の変形は，偏差の重み付き総和を最小化するというものである．特に，次の制約条件付最小化問題が解かれる．

ここで は実数 の正の部分を表す．重み は相対的な重要性を反映し，そう敵的なスケールおよび単位を考慮に入れるために偏差を正規化する．重みに対して可能な値は達成すべき目標の逆数である．上の問題は，解きやすい問題に再形式化することができる．

3つ目の変形はチェビシェフ目標計画法というもので，偏差の総和ではなく最大偏差を最小化する．これは異なる目的関数の偏差の均衡を保つ．特に，次の制約条件付き最小化問題を解くとする．

次のように再公式化することができる．

以下で，偏差の重み付き総和を最小化することにより目標計画法モデルを解く関数GoalProgrammingWeightedAverageを定義する：
下では，最大偏差を最小化することにより目標計画法モデルを解く関数GoalProgrammingChebyshevを定義する：
これは単位重量，目標からの結果の偏差が13.12および33.28（合計偏差37），最大偏差33.28のGoalProgrammingWeightedAverageを使い，2つの目的関数と1つの制約条件を持つ目的計画法問題を解く：
これは単位重量，目標からの結果の偏差が16および32，最大偏差32であるが合計偏差は38のGoalProgrammingChebyshevを使い，2つの目的関数と1つの制約条件を持つ目的計画法問題を解く：
以下は最初の目的関数（青），2つ目の目的関数（赤），実現可能領域（黒線），GoalProgrammingWeightedAverageで見付かった最適解（黄の点），GoalProgrammingChebyshevで見付かった最適解（緑の点）を示す：

適用例：ポートフォリオ最適化

投資管理のパワフルな方法は，相関関係がほとんど，あるいは全くない資産へ投資することでリスクを分配することである．例えば，ある年に資産Aは20%増加して翌年10%減少し，資産Bはある年に10%減少して翌年20%増加するというふうに，Aの上昇年はBの下降年とすると，両方を同じだけ保有していると，リスクなしで毎年10%の増加になる．実際にはそのような資産はほとんどあり得ないが，この考え方は役に立つものである．

この例の目的は，株，債権，金に投資して，リスクを最低限に抑え，事前設定したリターンを得るような最適資産分配を見付けるというものである．

次は1973年から1994年までのさまざまな資産のリターン歴である．例えば，1973年にはS&P 500は1-0.852=14.8%減少しているが，金は67.7%増加している．

"3m Tbill""long Tbond""SP500""Wilt.5000""Corp. Bond""NASDQ""EAFE""Gold"
19731.075`0.942`0.852`0.815`0.698`1.023`0.851`1.677`
19741.084`1.02`0.735`0.716`0.662`1.002`0.768`1.722`
19751.061`1.056`1.371`1.385`1.318`0.123`1.354`0.76`
19761.052`1.175`1.236`1.266`1.28`1.156`1.025`0.96`
19771.055`1.002`0.926`0.974`1.093`1.03`1.181`1.2`
19781.077`0.982`1.064`1.093`1.146`1.012`1.326`1.295`
19791.109`0.978`1.184`1.256`1.307`1.023`1.048`2.212`
19801.127`0.947`1.323`1.337`1.367`1.031`1.226`1.296`
19811.156`1.003`0.949`0.963`0.99`1.073`0.977`0.688`
19821.117`1.465`1.215`1.187`1.213`1.311`0.981`1.084`
19831.092`0.985`1.224`1.235`1.217`1.08`1.237`0.872`
19841.103`1.159`1.061`1.03`0.903`1.15`1.074`0.825`
19851.08`1.366`1.316`1.326`1.333`1.213`1.562`1.006`
19861.063`1.309`1.186`1.161`1.086`1.156`1.694`1.216`
19871.061`0.925`1.052`1.023`0.959`1.023`1.246`1.244`
19881.071`1.086`1.165`1.179`1.165`1.076`1.283`0.861`
19891.087`1.212`1.316`1.292`1.204`1.142`1.105`0.977`
19901.08`1.054`0.968`0.938`0.83`1.083`0.766`0.922`
19911.057`1.193`1.304`1.342`1.594`1.161`1.121`0.958`
19921.036`1.079`1.076`1.09`1.174`1.076`0.878`0.926`
19931.031`1.217`1.1`1.113`1.162`1.11`1.326`1.146`
19941.045`0.889`1.012`0.999`0.968`0.965`1.078`0.99`
average1.0781.0931.1201.1241.1211.0461.1411.130

次は毎年のリターンデータである：
これら8つの資産の22年間での予想リターンは次のようになる：
それぞれの資産が他とどのように相関があるかを測定する共分散行列である：
下で分配の標準偏差を最小にする最適資産分配を見付ける．ここで，分配合計は100% (Total[vars]==1)，想定リターンは12%以上 (vars.ER≥1.12)，変数は非負でなければならないという条件を前提にするため，各資産には非負のパーセンテージが割り当てられる（従ってリスクはない）．結果の最適資産割り当てでは，標準偏差0.0126で，3ヶ月の財務省短期債券に15.5%，金に20.3%，残りを株にするよう提案されている：
想定リターンを10%にすると，変動性が小さくなる代りにリターンも小さくなる．これでは，3ヶ月の財務省短期債券55.5%，金に10.3%，残りを株に割り当てることになる：

内点法の制限

FindMinimumで内点法を実装するには，目的関数と制約条件の第1および第2導関数が必要である．まず記号的導関数が試され，失敗すると有限差分を使って導関数が計算される．関数または制約条件が滑らかでない場合，特に最適点の第1導関数が連続でない場合は，内点法では収束しにくい可能性がある．

以下は，内点法では，滑らかでない関数を最小化するのが難しいことを示している：
以下は制約条件なしのニュートン法で見られる，類似の問題である：

制約条件付き局所的最適化の数値アルゴリズム

内点法

内点法は障壁関数を使って制約条件と目的関数を組み合せることにより，制約条件付き最適化を解く．特に，一般の制約条件付き最適化問題は，まず次の標準形式

および に変換される．次に非負の制約条件が，目的関数に障壁項を加えることにより置き換えられる．

ここで は障壁パラメータである．

例えば， の勾配が線形非依存であると仮定すると，必要なKKT条件は

であり，次元 × である．また は双対変数である．上記は以下のように書ける：

ここで は，対角要素が ならば の ，あるいはの対角行列である．また， は1のベクトルであり である．変数 を導入すると，上記の系は次のように書き換えられる：

また は対角要素が の対角行列である．この非線形系はニュートン法を使って解くことができる． および が成り立つとすると，上記の系(1)のヤコビ行列は次の通りである．

，を除去すると， になる．従って以下が成り立つ．

よって，制約条件付きの非線形問題は，

で反復的に解くことができる．このとき検索方向は上記のヤコビ系(2)を解くことで与えられる．

収束を確実なものにするために，成功の測定を行う必要がある．この方法のひとつにメリット関数を使うというものがある．次の拡張ラグランジュ(Lagrangian)メリット関数を使う．

拡張ラグランジュメリット関数

以下で，拡張ラグランジュメリット関数を定義する．

ここで は障壁パラメータ，はペナルティパラメータである．行列 が正定値行列ならば，(3)により与えられる検索方向が上記のメリット関数(4)について降順の方向であるか，がKKT条件(5)を満足するかのいずれかとなることが証明できる．正の制約条件を維持したままで，最初のステップ長ができるだけ1の近くに選ばれて線形探索が検索方向に沿って実行される．次に，Armijo条件がメリット関数 （ここで ）で満足するまで，バックトラック法が使われる．

収束誤差許容値

内点法の収束基準は

であり，tolはデフォルトで10-MachinePrecision/3に設定されている．