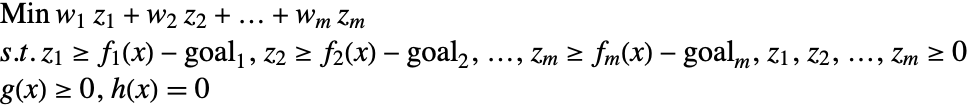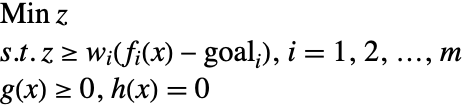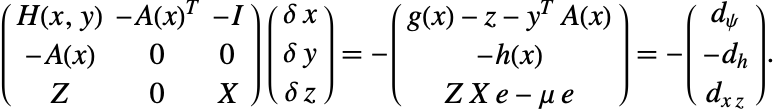数值非线性局部最优化

引言FindMinimum 的示例
FindMinimum 函数约束局部最优化的数值算法

引言

约束非线性优化的数值算法大致可分为基于梯度的方法和直接搜索方法. 梯度搜索方法使用一阶导数 (梯度) 或者二阶导数（黑塞(Hessians)矩阵）信息. 例如，序列二次规划 (SQP) 方法、增广拉格朗日方法和(非线性) 内点法. 直接搜索方法不适用导数信息. 例如，Nelder-Mead、遗传算法、差分进化以及模拟退火. 直接搜索方法往往收敛速度较慢，但是该方法对于函数和约束条件中噪声的存在较为宽容.     

通常情况下，算法只对问题建立局部模型. 此外，许多这种算法总是寻求目标函数的某种减小，或者寻求由目标函数和约束条件合成的一个优值函数的某种减小，来确保迭代过程的收敛. 如果收敛的话，这种算法只找到局部最优解，因而被称为局部优化算法. 在 Wolfram 语言里，局部优化问题可以通过使用 FindMinimum 求解.     

另一方面，全局优化算法通常通过既允许减小也允许增大目标函数/优值函数来试图求全局最优解. 通常这种算法的计算代价要更为昂贵. 全局优化问题可以使用 Minimize 精确求解，或者用 NMinimize 数值化地求解.

这里我们求解一个非线性规划问题， 利用 Minimize, 能够产生一个精确的解：
下面我们数值化地解同样的问题. NMinimize 给我们返回一个机器精度的解：
FindMinimum 数值化地求一个局部最小值. 在这个例子中找到的局部最小值也是全局最小值：

FindMinimum 函数

FindMinimum 求解局部非约束和约束最优化问题. 本文档只涵盖约束最优化的情况. 对于有关用于非约束优化问题的 FindMinimum 的详细信息，请参见 "非约束优化".

下面利用 FindMinimum 求解非线性规划问题， .
这里我们给 FindMinimum 提供 x 的初始值为 2，但是对于 y 我们使用默认的初始值.     

前面的解点实际上只是一个局部最小值. FindMinimum 只试图找到局部最小值.     

下面的可行域的等值线图显示了局部和全局最小值点：
这是在可行域内函数的一个三维演示图：

FindMinimum 的选项

FindMinimum 接受以下选项.

选项名
默认值
AccuracyGoalAutomatic所要达到的准确度
CompiledAutomatic函数和约束条件是否应该进行自动编译
EvaluationMonitorNone每当 f 被求值时，也被求值的表达式
GradientAutomatic梯度函数列表 {D[f,x],D[f,y],…}
MaxIterationsAutomatic所用的最大迭代次数
MethodAutomatic所使用的方法
PrecisionGoalAutomatic所要达到的精确度
StepMonitorNone每采取一个步骤时都要求值的表达式
WorkingPrecisionMachinePrecision在内部计算中所采用的精确度

FindMinimum 函数的选项.

Method 选项指定用来求解优化问题的方法. 目前，约束优化可以使用的唯一方法是 内点算法.

这里指定应该使用内点法：

MaxIterations 指定应该使用的最大迭代次数. 当约束优化使用机器精度的时候，则使用默认的MaxIterations->500.

指定 StepMonitor 后，在内点算法的每个迭代步骤里它都会被求值一次. 另一方面，当我们指定 EvaluationMonitor 时，每当一个函数或者一个等式或者不等式约束被求值时，它也会被求值.     

这里表明，19次迭代不足以在默认的容差范围内解决下面的问题. 通过 StepMonitor 的使用，它可以收集所有访问过的点：
用 ContourPlot 来显示访问过的点. 初始点是蓝色的，其余点是黄色的.     

WorkingPrecision->prec 规定 FindMinimum 里的所有计算都必须在精确度 prec 上执行. 默认情况下， prec=MachinePrecision. 如果 prec>MachinePrecision，在计算过程中，则使用一个固定的精确度 prec.

AccuracyGoal 和 PrecisionGoal 选项以下列方式使用. 默认情况下，AccuracyGoal->Automatic，而且被设置为 prec/3. 默认情况下，PrecisionGoal->Automatic 并且被设置为 -Infinity. AccuracyGoal->ga 和 AccuracyGoal->{-Infinity,ga} 相同.     

假设 AccuracyGoal->{a,ga} 并且 PrecisionGoal->p，那么 FindMinimum 试图使残差小于或者等于 tol=10-ga，该残差是可行性和对Karush-Kuhn-Tucker(KKT)以及补充条件的满足的一个组合. 此外，它还要求在终止前，当前和下一个迭代点 x 和 x+ 的差满足 .     

这里使用一个值为100的 WorkingPrecision 计算问题的解.     
使用 Minimize 计算确切的优化值并与 FindMinimum 的结果比较：

FindMinimum 的示例

求解全局最小值

如果需要一个全局最小值，则应该使用 NMinimize 或者 Minimize. 然而，因为 FindMinimum 的每次运行往往快于 NMinimize 或者 Minimize，有时候使用 FindMinimum 更为有效，尤其对于具有少数局部最小点的相对较大的问题. FindMinimum 试图找到一个局部最小值，因此如果找到一个局部最小值，它将会终止.

这里显示一个在可行域 -10≤x≤10 内具有多个极小点的函数.     
由自动选择的初始点，FindMinimum 收敛到一个局部极小值：
如果用户对于该问题有一些了解，就可以给 FindMinimum 提供更好的初始点：
另一种方法是，用户也可以加强约束条件：
最后，我们可以使用多个初始点然后选择最佳极小值：
利用 "RandomSearch" 方法，并使用内点法作为后处理器，多个初始点也可以通过 NMinimize 更系统地处理.     

求解 Minimax 问题

Minimax (也称为 minmax) 问题是寻找被定义为一些函数极大值的一个函数的极小值，也就是说，    

虽然这个问题往往可以利用一般约束优化技术求解，把问题重新定义为一个平稳目标函数则更为可靠. 具体来说，minimax 问题可以转化成以下形式

并且利用 FindMinimum 或者 NMinimize 求解.

这里定义一个函数 FindMinMax：
这里求解一个具有单变量的非约束 minimax 问题：
这里求解一个具有两个变量的非约束 minimax 问题：
这里显示了目标函数的等值线图和最优解：
这里求解一个约束 minimax 问题：
这里显示了可行域内目标函数的等值线图，以及最优解：

多目标优化: 目标规划

多目标规划包括在约束条件下极小化多个函数. 由于极小化一个函数的解不总是同时极小化其他函数，所以通常我们的问题没有单一的最优解.

有时候，决策者心目中已经对每个目标函数有一个目标. 在这种情况下，则可以应用所谓的目标规划技术.

建立目标规划问题模型的方法有好几种变种. 其中一个变种是依据优先级对目标函数进行排序，并且首先寻求最重要目标函数对其目标的偏差的极小化，然后再尝试次要目标函数对其目标的偏差的极小化. 这被称为字典或者preemptive 目标规划.

第二个变种，是将偏差的加权和极小化. 具体地说，就是要解下面的约束极小化问题.

这里 代表实数 的正数部分. 权重 反映了相对重要性，并且对偏差进行规范化以便把相对尺度和单位考虑在内. 权重的可能值是要实现的目标的倒数. 我们可以把前面的问题改写为一个容易求解的问题.

第三个变种，切比雪夫目标规划，极小化最大偏差，而不是偏差的总和. 这种方法均衡了不同目标函数的偏差. 具体地说，是要求解下面约束极小化问题.

这可以改写为:

这里定义一个函数 GoalProgrammingWeightedAverage 以通过极小化偏差的加权和来求解目标规划模型：
这里定义一个函数 GoalProgrammingChebyshev 以通过极小化最大偏差来求解目标规划模型：
这里通过单位加权的 GoalProgrammingWeightedAverage 求解有两个目标函数和一个约束条件的目标规划问题，所得与目标间的偏差为13.12和33.28，因此总偏差为37，而最大偏差33.28：
这里通过单位加权的 GoalProgrammingChebyshev 求解有两个目标函数和一个约束条件的目标规划问题，所得与目标间的偏差为16和32，因此最大偏差为32，但总偏差为38.     
这里图示了第一个目标函数(蓝色)和第二个目标函数(红色)，可行域(黑线)，以及通过GoalProgrammingWeightedAverage 找到的最优解(黄点) 和通过 GoalProgrammingChebyshev 找到的最优解(绿点).     

一个应用实例：投资组合优化

一个投资管理的有力工具是通过投资很少或根本没有关联的资产来分散风险. 例如，如果资产A一年上升20%，第二年下降10%，而资产B一年下降10%，第二年上升20%，并且A的上升年份是B的下降年份，那么拥有同等数量的两份资产将导致每年有10%的增加率，没有任何风险. 在现实中这种资产很少，但是这一概念仍然是有益的.

在这个例子中，目的是通过投资于分散的股票、债券、黄金找到最佳的资产分配，以使风险最小化，并且实现预定的回报.

以下是在1973年和1994年之间各种资产的历史回报率. 例如，在1973年，标准普尔500指数跌 1-0.852=14.8%，而黄金升值67.7%.

"3m Tbill""long Tbond""SP500""Wilt.5000""Corp. Bond""NASDQ""EAFE""Gold"
19731.075`0.942`0.852`0.815`0.698`1.023`0.851`1.677`
19741.084`1.02`0.735`0.716`0.662`1.002`0.768`1.722`
19751.061`1.056`1.371`1.385`1.318`0.123`1.354`0.76`
19761.052`1.175`1.236`1.266`1.28`1.156`1.025`0.96`
19771.055`1.002`0.926`0.974`1.093`1.03`1.181`1.2`
19781.077`0.982`1.064`1.093`1.146`1.012`1.326`1.295`
19791.109`0.978`1.184`1.256`1.307`1.023`1.048`2.212`
19801.127`0.947`1.323`1.337`1.367`1.031`1.226`1.296`
19811.156`1.003`0.949`0.963`0.99`1.073`0.977`0.688`
19821.117`1.465`1.215`1.187`1.213`1.311`0.981`1.084`
19831.092`0.985`1.224`1.235`1.217`1.08`1.237`0.872`
19841.103`1.159`1.061`1.03`0.903`1.15`1.074`0.825`
19851.08`1.366`1.316`1.326`1.333`1.213`1.562`1.006`
19861.063`1.309`1.186`1.161`1.086`1.156`1.694`1.216`
19871.061`0.925`1.052`1.023`0.959`1.023`1.246`1.244`
19881.071`1.086`1.165`1.179`1.165`1.076`1.283`0.861`
19891.087`1.212`1.316`1.292`1.204`1.142`1.105`0.977`
19901.08`1.054`0.968`0.938`0.83`1.083`0.766`0.922`
19911.057`1.193`1.304`1.342`1.594`1.161`1.121`0.958`
19921.036`1.079`1.076`1.09`1.174`1.076`0.878`0.926`
19931.031`1.217`1.1`1.113`1.162`1.11`1.326`1.146`
19941.045`0.889`1.012`0.999`0.968`0.965`1.078`0.99`
average1.0781.0931.1201.1241.1211.0461.1411.130

这是年度回报率数据：
下面是22年期间这八个资产的预期回报率：
下面是协方差矩阵，测量各种资产如何互相关联：
这里通过极小化每个配置的标准偏差来找到最佳资产配置，其相应的约束条件为拨款总额为100% (Total[vars]==1)，预期收益超过12% (vars.ER≥1.12)，以及变量必须非负，因此每项资产分配一个非负的百分比(因而没有放空). 由此产生的最佳资产分配表明15.5%应投资于3个月的国库券，20.3%应投资于黄金，剩下的应投资于股票，此结果的标准差为0.0126：
这里通过要求10%的预期收益来用较少的回报交换较小的波动性. 现在我们有55.5%的投资在3个月的国库券，10.3%在黄金，而其余的在股票：

内点法的局限性

在 FindMinimum 中内点法的实现需要用目标函数和约束条件的一阶和二阶导数. 计算导数时首先尝试符号式计算，如果失败的话，则使用有限差分来计算导数. 如果函数或者约束条件不是平滑的话，特别是如果在最优点的一阶导数不是连续的话，内点法可能会在收敛上遇到困难.     

下面显示内点法在极小化非平滑函数上有困难：
这有点类似于非约束牛顿法遇到的困难：

约束局部最优化的数值算法

内点算法

内点算法通过利用障碍函数组合约束条件和目标函数来求解约束优化问题. 具体来说，一般约束最优化问题首先转换为标准格式

且 . 然后通过向以下目标函数添加障碍项来替换非负约束：

其中 是一个障碍参数.

必要的KKT条件(例如，假设梯度 是线性无关的)为     

其中 的维数为 ×，且 是对偶变量. 前式可以写成：

其中 是对角矩阵，若 ， 的对角元素为 ，否则为 ，且 是 1 的向量，且 . 引入变量 ，前面的系统可以改写为：

且 为对角元素为 的对角矩阵. 该非线性系统可以用牛顿法求解. 令 且，系统 (1) 的雅可比矩阵为

消去 ，，有 ，因而

因此, 非线性约束问题可以通过如下方法迭代地求解     

其搜索方向 由求解前面的雅克比方程组(2)得到.     

为了确保收敛，您需要对是否成功有某种测量方法. 其中一个方法是利用一个优值函数，如下面的增广拉格朗日优值函数.

增广拉格朗日优值函数

这里定义一个增广拉格朗日优值函数

这里 是障碍参数而 是一个罚参数. 可以证明，如果矩阵 是正定的，那么要么由(3)提供的搜索方向都是上述优值函数(4) 的下降方向，要么 满足了 KKT 条件(5). 沿着搜索方向，我们进行线搜索，初始步长尽可能的接近1，同时保持约束条件为正值. 然后应用回溯程序直至优值函数满足Armijo条件， 其中 .

收敛容差

内点法的收敛标准是

其中 tol 被默认地设置为 10-MachinePrecision/3.