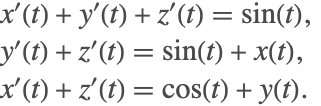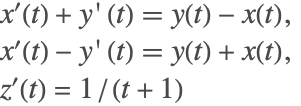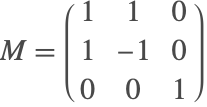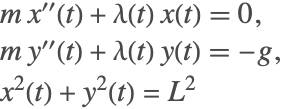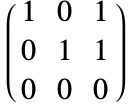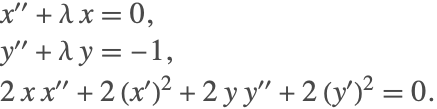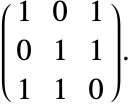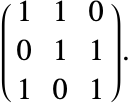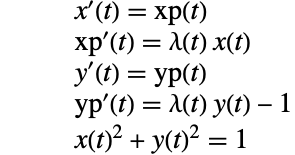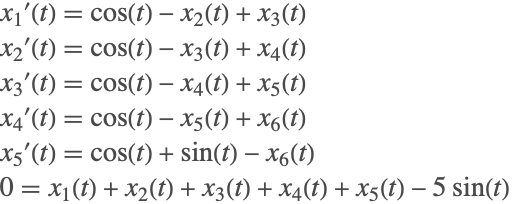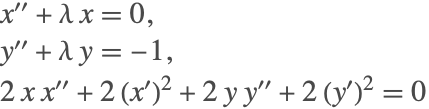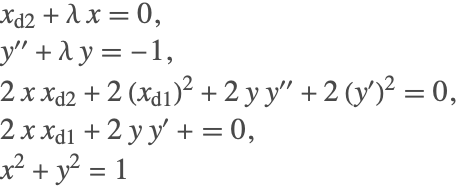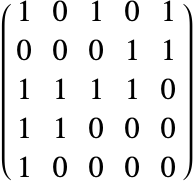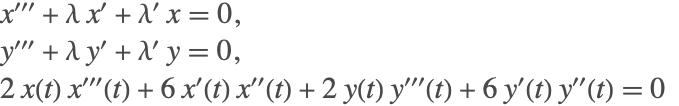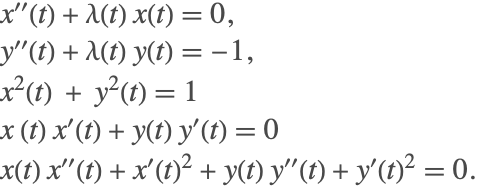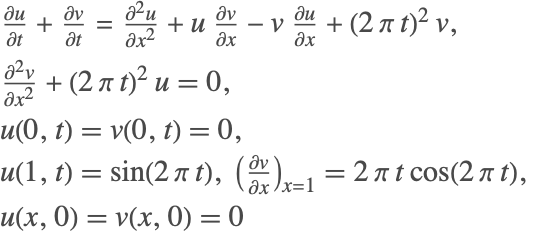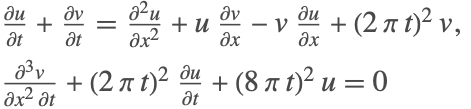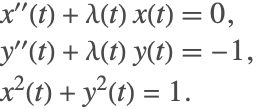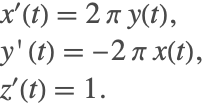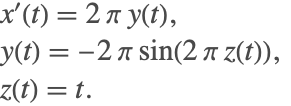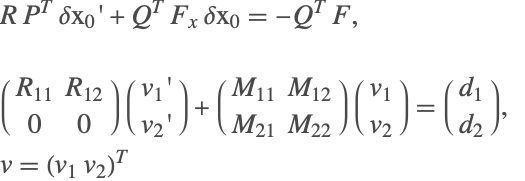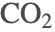微分代数方程式の数値解法
はじめに
で表すことができる.従属変数 ![]() の導関数は,過渡的な独立変数
の導関数は,過渡的な独立変数 ![]() と従属変数
と従属変数 ![]() について明示的に表される.関数
について明示的に表される.関数 ![]() に十分な連続性がある限り,従属変数の値が独立変数の特定の値において与えられるという初期値問題に対する一意解は常に見付けることができる.
に十分な連続性がある限り,従属変数の値が独立変数の特定の値において与えられるという初期値問題に対する一意解は常に見付けることができる.
微分代数方程式では,一般に導関数は明示的に表されない.実際,従属変数の中にはその導関数が通常方程式に現れないものもある.例えば,以下の方程式
には ![]() の導関数が明示的には含まれていない.このような変数は代数的変数と呼ばれることがよくある.
の導関数が明示的には含まれていない.このような変数は代数的変数と呼ばれることがよくある.
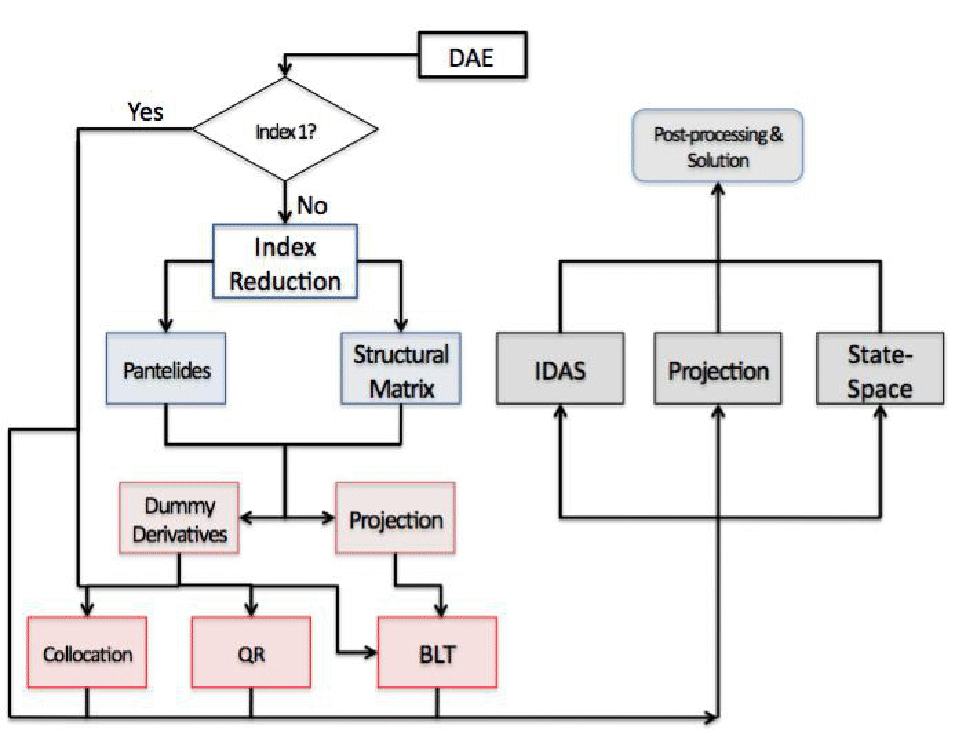
微分代数方程式系を解くには,多数のステップが必要となることが多い.以下のフローチャートはNDSolveで微分代数方程式を解くことに関する一般的なプロセスを示すものである.
NDSolveで微分代数方程式系を解くのに関わるプロセスを示すフローチャート
通常,微分代数方程式系は独立変数 ![]() について微分することで常微分方程式系に変換することができる.微分代数方程式の指数とは,常微分方程式系を得るために微分代数方程式系を微分する回数である.
について微分することで常微分方程式系に変換することができる.微分代数方程式の指数とは,常微分方程式系を得るために微分代数方程式系を微分する回数である.
NDSolveに組み込まれている微分代数方程式ソルバは,指数1の系に使うものなので,高指数の系の場合は解を得るために指数減少法が必要になる場合がある.NDSolveは指数減少法を実行することができる.系に1より大きい指数が含まれていると,NDSolveは微分代数方程式を解くために必要なメッセージとステップ数を出力する.
高指数の微分代数方程式での第1ステップは,系の指数を減少させることである.指数を減少させるために微分するプロセスは,指数減少法と呼ばれ,NDSolveの記号的プロセスで実行できる.
指数減少法のプロセスによって,新しい同等の系になる.1つのアプローチでは,この新しい系は微分された変数の代りに新しい(ダミー)変数を代入することにより構築される.これだと,一意に解くことのできる拡張された系になる.別のアプローチでは,すべての変数に対する微分が構築されるまで,もとの系を ![]() 回微分する.先行する
回微分する.先行する ![]() 回微分された系は,不変量として扱われる.
回微分された系は,不変量として扱われる.
この新しい指数減少系を解くためには,矛盾のない初期条件集合を見付けなければならない.標準形の常微分方程式系 ![]() は常に,開始時に
は常に,開始時に ![]() の値を与えることにより初期化することができる.しかし.微分代数方程式の場合は残差方程式
の値を与えることにより初期化することができる.しかし.微分代数方程式の場合は残差方程式 ![]() を満足する初期条件を見付けることは難しいことがある.これは結局,変数のいくつかだけが独立して指定されている非線形の代数系を解くことになるのである.このことに関しては後のセクションで詳しく説明する.さらに,初期化は一貫していなければならない.つまり,残差方程式の微分
を満足する初期条件を見付けることは難しいことがある.これは結局,変数のいくつかだけが独立して指定されている非線形の代数系を解くことになるのである.このことに関しては後のセクションで詳しく説明する.さらに,初期化は一貫していなければならない.つまり,残差方程式の微分 ![]() も満足されなければならないのである.通常,高指数の系になるほど初期化が難しい.この場合,一般にNDSolveでは
も満足されなければならないのである.通常,高指数の系になるほど初期化が難しい.この場合,一般にNDSolveでは ![]() の要素がどのように相互作用を及ぼし合うか見ることができないので,指数減少が自動でできない.しかし,NDSolveには,オプションを介して利用できる,指数減少を実行し,微分代数方程式の矛盾のない初期化を見付けるためのさまざまなメソッドがある.
の要素がどのように相互作用を及ぼし合うか見ることができないので,指数減少が自動でできない.しかし,NDSolveには,オプションを介して利用できる,指数減少を実行し,微分代数方程式の矛盾のない初期化を見付けるためのさまざまなメソッドがある.
このドキュメントの残りの部分は次のようになっている.まず微分代数方程式の指数に関連した用語を紹介し,次に指数1の微分代数方程式の解き方を説明する.その次に高指数の微分代数方程式の指数減少法を説明する.微分代数方程式の矛盾のない初期化も扱う.ここまでの例題に加え,最後のセクションではさらに例題を提示する.
微分代数方程式の指数
一般的な微分代数方程式系 ![]() では,系の指数とは
では,系の指数とは ![]() および
および ![]() について一意に
について一意に![]() を解くために必要な,系に含まれる方程式の一部あるいはすべてを微分する最小回数である.文献では指数の考え方について多少異なるものもあるが,このドキュメントでは,上記の考えを使う.
を解くために必要な,系に含まれる方程式の一部あるいはすべてを微分する最小回数である.文献では指数の考え方について多少異なるものもあるが,このドキュメントでは,上記の考えを使う.
![]() の微分方程式を得るためには,最初の方程式を1回微分しなければならない.これで,新しい系ができる.
の微分方程式を得るためには,最初の方程式を1回微分しなければならない.これで,新しい系ができる.
微分された方程式系には,説明の必要な ![]() が含まれている.
が含まれている.![]() の方程式を得るために,2つ目の方程式は3回微分しなければならない.これにより以下が得られる.
の方程式を得るために,2つ目の方程式は3回微分しなければならない.これにより以下が得られる.
系の一部は ![]() の導関数方程式を得るために3回微分しなければならないので,この微分代数方程式の指数は3である.微分された最終的な系は,指数0の系と言われる.微分によって得られた常微分方程式系を見るためには,適切な代入を行わなければならない.この場合は最初の方程式から2つ目の方程式を引くことである.結果の方程式は次のように書くことができる.
の導関数方程式を得るために3回微分しなければならないので,この微分代数方程式の指数は3である.微分された最終的な系は,指数0の系と言われる.微分によって得られた常微分方程式系を見るためには,適切な代入を行わなければならない.この場合は最初の方程式から2つ目の方程式を引くことである.結果の方程式は次のように書くことができる.
同様に,指数1の系は2つ目の方程式を2回微分することにより見付けることができ,以下の系となる.
系の指数を1に減少させるというのは一般的なことである.内在する積分ルーチンがそれを効率的に扱えるからである.
微分代数方程式の指数は明らかでない場合がある.これは初期条件が何であるかにより,指数1あるいは指数2の動作を見せる可能性のある系を考える.
この微分代数方程式では,2つ目の方程式で ![]() が0か1であることが要求されているため初期条件は無ではない.
が0か1であることが要求されているため初期条件は無ではない.
![]() ならば,残りの2つの方程式は指数1の系になる.3つ目の方程式の微分が2つの常微分方程式系を与えるからである.
ならば,残りの2つの方程式は指数1の系になる.3つ目の方程式の微分が2つの常微分方程式系を与えるからである.
一方,![]() ならば,残りの2つの方程式は指数2の系になる.3つ目の方程式の微分が
ならば,残りの2つの方程式は指数2の系になる.3つ目の方程式の微分が ![]() を与え,それを最初の方程式に代入すると
を与え,それを最初の方程式に代入すると ![]() になる.これを微分して常微分方程式を得る.
になる.これを微分して常微分方程式を得る.
この例は,必要な初期条件の数と微分代数方程式の指数の両方が,実際に見付けられる解に影響を及ぼすことを示している.
微分方程式の取扱い
微分方程式を解くために,NDSolveはユーザが指定した系を3つの形式のいずれかに変換する.系がどのように構築されるかにより.異なる積分法が選ばれるので,このステップは非常に重要である.
オプションMethod->{"EquationSimplification"->simplification}を使うと,どの形式で方程式を表すかを指定することができる.次の簡約化メソッドは,"EquationSimplification"オプションに対して指定することができる.
| Automatic | 系を形式 |
| "Solve" | 可能であれば,系を形式 |
| "MassMatrix" | 可能であれば,系を形式 |
| "Residual" | 方程式の左辺から右辺を引いて,残差関数 |
デフォルトでは独立変数 ![]() と従属変数
と従属変数![]() に関して明示的に導関数
に関して明示的に導関数![]() について解くことが試みられる.効率を考えて,NDSolveはまずLinearSolveを使って明示的な系を見つけようとする.しかし,それに失敗すると,Solveを使って記号的に系が解かれる.
について解くことが試みられる.効率を考えて,NDSolveはまずLinearSolveを使って明示的な系を見つけようとする.しかし,それに失敗すると,Solveを使って記号的に系が解かれる.
"Solve"メソッドを使うことは記号解が見付けるときのデフォルトと同じである.
系が残差形式になると,導関数は一意のシンボルとなるよう生成された新しい変数集合によって表される.NDSolveStateDataの"Variables"プロパティと"WorkingVariables"プロパティを使うと,これらの作業変数と指定された変数の間の対応が分かる.
明示的な常微分方程式系を生成する過程は,システムの記号的取扱いにより高価になる場合がある.このため,方程式を得るのに1秒という時間制限がある.この時間を超えると,NDSolveはメッセージを生成し,啓を微分代数方程式として解こうとする.
次のメソッドオプションは,簡約化メソッドに指定して"EquationSimplification"の動作をよりよく制御することができる.
オプション名
|
デフォルト値
| |
| "TimeConstraint" | 1 | Solveが導関数を明示的に解くのに許された最大時間(秒) |
| "SimplifySystem" | False | できるだけ多くの従属変数について解析解を得ることで簡約化するかどうか |
メッセージに示されているように,Solveが1秒というデフォルトの時間制限を超えていたのでNDSolveはこの導関数について明示的に解かなかった.NDSolveが明示的な式を得るのにかける時間は,オプション"TimeConstraint"で制御することができる.
上の例では,最初の方程式に二次項があるため,可能性のある4つの解が得られる.微分代数方程式として解く場合,どのように初期化されるかによって,数値解はこれらの解のいずれか一つに従う.
メソッドオプション"SimplifySystem"の使い方を示すために,次の例題を考える.
上記の系の解析解は,![]() の解を求めるために
の解を求めるために ![]() を最初の方程式に代入することで得られる.次にこれを
を最初の方程式に代入することで得られる.次にこれを ![]() の解を得るために第2の方程式に代入する.最終的な系の解は次のようになる.
の解を得るために第2の方程式に代入する.最終的な系の解は次のようになる.
NDSolveは,まず系の指数減少を実行して等価となる新しい常微分方程式系を形成してからでないと,この系を解くことはできない.これは高価になることを意味し得る.サブオプションの"SimplifySystem"を有効にすると,NDSolveは解析式または解析解が見付かる変数をすべて検出し,もとの系に繰り返し代入し続ける.この結果,もとの系は簡約化されるか,場合によっては(上記のように)解析解に戻る.
ある変数に対して解析解が存在しない場合は,NDSolveは解として補間関数を返す.
サブオプションを有効にすると,定数パラメータは系に直接代入することができる.
微分代数方程式の解法
NDSolveには,微分代数方程式を解くためのさまざまな解法が組み込まれている.
指数1の微分代数方程式の一般的な残差形式 ![]() には2つの方法が使える.
には2つの方法が使える.
- StateSpace—導関数
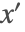 について暗示的に
について暗示的に  を解き,内在する常微分方程式ソルバを使う.
を解き,内在する常微分方程式ソルバを使う.
系が指数2以上である場合,これらのソルバはどちらも失敗する.そのような系を正確に解くためには,指数減少法が必要である.指数1の系は常微分方程式に簡約できるが,上のソルバのどちらかを使った方が効率がよい.
NDSolveは,特殊形式に簡約することのできる微分代数方程式に使えるソルバも備えている.
- Projection—不変量
 の常微分方程式
の常微分方程式 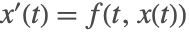 用
用
不変量のある常微分方程式
微分代数方程式系が指数減少法によって常微分方程式に変換されると,常微分方程式を得るために微分された方程式は,その常微分方程式に矛盾しない.解は積分されるので,これらの方程式が満足されることを確実にすることは通常大切なことである.
このような系は未知数よりも多い方程式を持ち,制約条件が常微分方程式と矛盾していれば過剰決定系である.NDSolveは同数の方程式と従属変数を持つ系を想定しているため,そのような微分代数方程式は扱わない.そのような系を解くために,NDSolveに組み込まれている"Projection"メソッドが各ステップごとに計算された解を![]() に投影することによって不変量を扱う.これにより,解が進化するにつれて確実に代数方程式は満足する.
に投影することによって不変量を扱う.これにより,解が進化するにつれて確実に代数方程式は満足する.
このような制約条件付きの系の例には,振り子の動作をモデル化する非線形振動子がある.
微分方程式は不変量の導関数であるため,この方程式を解く一つの方法は,不変量を使うことである.
質量行列を持つ系を解く
ここで ![]() は質量行列と言われることの多い行列である.
は質量行列と言われることの多い行列である.![]() は減衰行列と呼ばれることもある.行列が非特異ならば,転置して,系を常微分方程式として解くことができる.しかし,特異行列がある場合は,系は微分代数方程式として解くことができる.どちらの場合も特殊形式を使うと利点が多い.
は減衰行列と呼ばれることもある.行列が非特異ならば,転置して,系を常微分方程式として解くことができる.しかし,特異行列がある場合は,系は微分代数方程式として解くことができる.どちらの場合も特殊形式を使うと利点が多い.
微分代数方程式の指数減少
NDSolveの微分代数方程式用の組込みソルバは現在完全に自動的に指数1の微分代数方程式を扱う.高指数の系では,解を得るために指数減少が必要である.この指数減少はNDSolveに適切なオプションを与えることで実行することができる.
NDSolveは記号的手法を使って指数減少を実行する.つまり,微分代数方程式系が ![]() という形式で表されるならば,ここでNDSolveは
という形式で表されるならば,ここでNDSolveは ![]() の要素がどのように相互作用を及ぼし合い,記号的導関数を計算するのかを見ることができず,指数減少は行えない.このためNDSolveはデフォルトでは指数減少を実行しないのである.
の要素がどのように相互作用を及ぼし合い,記号的導関数を計算するのかを見ることができず,指数減少は行えない.このためNDSolveはデフォルトでは指数減少を実行しないのである.
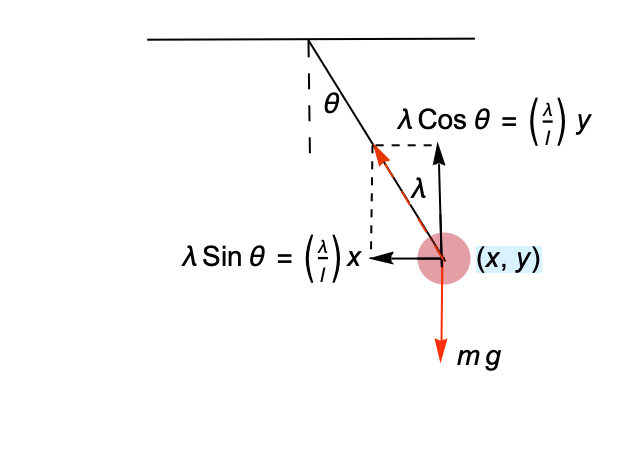
例として,振り子の動きを記述する古典的な微分代数方程式を考えてみる.
ここで紐の長さ ![]() によって制約される点
によって制約される点![]() における質量
における質量 ![]() がある.
がある.![]() は実質的に紐の張力であるラグランジュ乗数である.指数減少の説明を簡単にするために,
は実質的に紐の張力であるラグランジュ乗数である.指数減少の説明を簡単にするために,![]() としよう.以下の図は振り子の系の略図である.
としよう.以下の図は振り子の系の略図である.
系の指数が方程式から明確でない場合,できることはNDSolveで試してみることである.ソルバで解けないときは,多くの場合指定された初期条件に対してどのような指数が現れるかを示すメッセージが生成される.

このメッセージは指数が3であるということを示し,系を解くためには指数減少が必要であるといっている.ここでは,初期化で起こり得る問題を避けるために,完全に矛盾のない初期化が使われる.解法のこの部分は,「微分代数方程式の矛盾のない初期化」で扱う.
NDSolveが,一般的な指数減少オプション iropts で指数減少法 irmeth を使うように指定するためには,オプション設定Method->{"IndexReduction"->{irmeth,iropts}}を使う.
| None | 指数減少なし(デフォルト) |
| Automatic | 自動的にメソッドを選択する |
| "Pantelides" | グラフベースのPantelidesアルゴリズム |
| "StructuralMatrix" | 構造行列ベースのアルゴリズム |
指数減少は,微分代数方程式系の方程式を微分することによって実行される.deqn=![]() eqn が eqn の代りに系に含まれるように,指数減少法の過程で,方程式 eqn が微分されるとする.微分が終了すると,微分された方程式は完全決定系を構成し,自分で解くことができる.しかし,系の中に制約条件としてもとの方程式を含ませるのは通常大切なことである.これは指数減少オプションの"ConstraintMethod"で制御される.
eqn が eqn の代りに系に含まれるように,指数減少法の過程で,方程式 eqn が微分されるとする.微分が終了すると,微分された方程式は完全決定系を構成し,自分で解くことができる.しかし,系の中に制約条件としてもとの方程式を含ませるのは通常大切なことである.これは指数減少オプションの"ConstraintMethod"で制御される.
| None | もとの方程式を制約条件として維持せず,差分方程式だけで解く |
| "DummyDerivatives" | MattsonとSoderlind [MS93]の方法を使い,いくつかの導関数を代数変数(ダミー導関数)で置き換える |
| "Projection" | 指数を0に減少させて常微分方程式を得,不変量として微分されたもとの方程式で"Projection"時間積分メソッドを使う |
微分された方程式だけの数値解では,振り子の長さが1から離れていく.もとの方程式を制約条件として解に含ませることは,指数減少の大切な一面である.
次の2つのセクションでは指数減少アルゴリズムと,NDSolveで使うことのできる制約メソッドについて説明する.
指数減少法
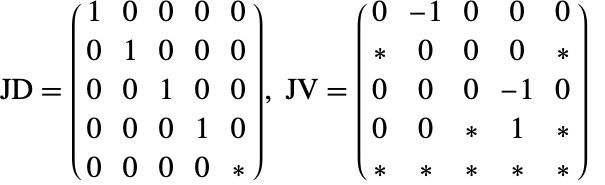
NDSolveには指数減少を行うアルゴリズムとしてPantelides法と構造行列法の2つがある.これらの方法は両方とも方程式の記号形式を使ってどの方程式を微分するかを決定し,記号的微分を使って微分された系を得る.
どちらの方法も方程式の構造的な接続の概念を使っている.特に,変数 ![]() が方程式
が方程式 ![]() に明示的に現れたら,
に明示的に現れたら,![]() は
は ![]() のtermed incidentである.構造的な接続行列とは,
のtermed incidentである.構造的な接続行列とは,![]() が
が ![]() の接続ならば,要素
の接続ならば,要素 ![]() を持ち,それ以外の場合は
を持ち,それ以外の場合は ![]() を持つ行列である.対角要素に1が存在するように構造的接続行列を並べ替えることができるならば,微分代数方程式系は構造的指数1を持つ.このような並替えができるということは,各変数に対して1つの方程式があるように,方程式と変数の間の対応が存在するということを意味している.
を持つ行列である.対角要素に1が存在するように構造的接続行列を並べ替えることができるならば,微分代数方程式系は構造的指数1を持つ.このような並替えができるということは,各変数に対して1つの方程式があるように,方程式と変数の間の対応が存在するということを意味している.
Pantelides法は,非常に大きな系でも効率的であり得る接続に基づいたグラフに使える.
構造的な指数は,その系の実際の指数よりは小さい場合があることに注意する.実際の系では,構造的に存在する項がいくつかの解とともに消滅するか,ヤコビ行列が特異であるかする可能性がある.構造行列法は,ヤコビアンに特異性がある可能性を考慮し,系によってはよりよい指数減少を実行するが,計算費用は大きくなる.
次のセクションでは,Pantelides法の説明に便利な構造的接続行列を得るコマンドを紹介し,その次のセクションでは構造行列法について説明する.
構造的接続行列
| NDSolve`StructuralIncidenceArray[eqns,vars] | 方程式 eqns の変数 vars に対する構造的接続行列のパターンを持つSparseArrayを返す |
SparseArrayはメモリ使用量が少なくてすむ非零のパターンだけを含んでいる.これは接続のパターンを表すことを意味する.ArrayRulesを使うと,1のSparseArrayに変換することができる.
ここでは対角要素の零を避けるのに並替えが必要ないので,この系は構造的指数1を持つ.
導関数変数についての構造的並替えで,対角要素に零を避けるよう並べ替えられるならば,この系は指数0である.
対角要素で零を避ける並替えはない.しかし,2つ目の方程式が微分されるとこれは可能になる.
微分された系が構造的指数0を持つので,もとの系は指数1であることが証明される.
もう一つの例として制約条件付きの振り子(2)を考える.
この行列は対角要素の零要素を避けるために並べ替えることができないので,指数は1より大きい.
関数NDSolve`StructuralIncidenceArrayは接続をチェックするために,式のFullFormで文字のマッチングを行うだけである.この関数は,方程式や変数が適切な形であるかどうかのチェックはしない.
x'[t]のFullFormが x を含むDerivative[1][x][t]なので,これは完全行列である.
Pantelides法
Pantelidesによって提唱された方法[P88]は,もとは微分代数方程式の矛盾のない初期化を求めるために提唱されたグラフ理論的なメソッドである.これは従属変数と方程式の二部グラフに使うことができ,アルゴリズムがグラフを走査すると,系は最大で指数1に簡約される.ここでの走査とは,指数行列の対角線上にゼロがないような変数と方程式の順序を指す.
二部グラフに完全走査がない場合,アルゴリズムは方程式を微分することで経路を拡大し,その過程で新しい変数(前の変数の導関数)を導入する.もとの系が構造的に特異でなければ,アルゴリズムは走査で終了する.通常アルゴリズムは走査に必要な微分だけを行うが,これは貪欲法なので,常に最小数とは限らない.
このアルゴリズムの詳細は,このドキュメントでは割愛する.Wolfram言語に組み込まれている実装は,[P88]で説明されているアルゴリズムに密接に従っている.これはGraphを使ってグラフ計算を実装し,微分が求められたときはDを使って方程式を記号的に微分する.
系の走査があるときは,指数行列がブロック下三角形式になるような変数と方程式の順序を見付けることが可能である.ブロック下三角形式は制約条件を維持するためのダミー導関数メソッドの設定において,また"StateSpace"時間積分メソッドにおいても使われる.ブロック下三角行列の順序に関する詳細は,「微分代数方程式の状態空間法」をご覧いただきたい.
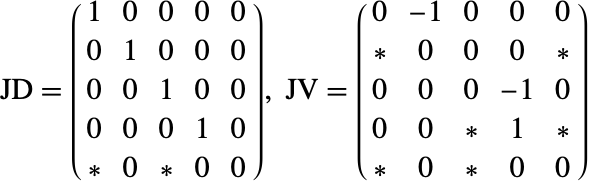
振り子系の指数減少法(2)を始めるために,変数![]() を考える.通常,方程式に現れる最高階の導関数から開始する.振り子方程式は以下の通りである.
を考える.通常,方程式に現れる最高階の導関数から開始する.振り子方程式は以下の通りである.
また,最高階数の導関数についてのグラフ接続行列は以下である.
接続行列は方程式の変数の存在をチェックすることによって構築される.方程式に変数が存在する場合,重み1が与えられ,存在しない場合は0が指定される.したがって,最初の方程式の変数![]() のチェックで
のチェックで![]() が得られる(接続行列の最初の行に見られるとおりである).
が得られる(接続行列の最初の行に見られるとおりである).
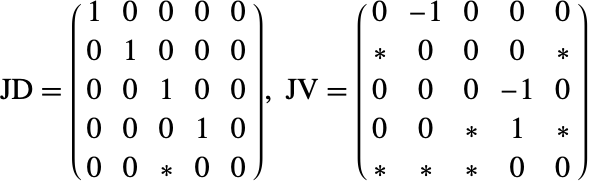
最初の接続行列から,走査がないことが分かる.最後の方程式は2回微分される.
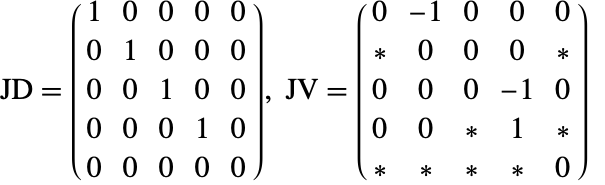
これは,結果として接続行列になる最初と最後の方程式を入れ替えることによって対角要素に0がないように並べ替えることができる.
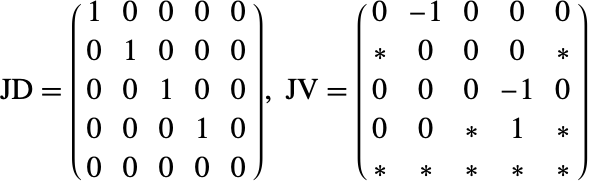
結果の系の指数は1(![]() がまだ代数的変数として現れるため)であり,微分された系に導関数を含まない.もう一度系を微分することによって
がまだ代数的変数として現れるため)であり,微分された系に導関数を含まない.もう一度系を微分することによって ![]() の微分系が与えられる.ゆえに,もとの系の指数は3となる.
の微分系が与えられる.ゆえに,もとの系の指数は3となる.
最初のアプローチとして2回微分された方程式を持つ系は直接解くことができる.
もとの振り子の長さの制約条件はあまりよく満足されておらず,実際には伸びている.新しい系がもとの系を方程式を完全に等しく表していないので,制約条件は十分満足しないのである.これは新しい系にもとの制約条件![]() ではなく,微分された方程式が含まれているという事実から分かる.
ではなく,微分された方程式が含まれているという事実から分かる.
新しい系を持つもとの系の力学をモデル化するためには,追加の方程式が満足されなければならない.しかし,追加の方程式を含めることは未知数よりも方程式が多くなる.この問題を解決するために,指数減少された系が平衡となるよう,ダミー導関数の方法が使われる.
Pantelidesアルゴリズムは,非常に大きい問題に対してもよく制御された複雑性を備えたグラフアルゴリズムを使うことができるので,効率的である.しかし,これは事象に基づいているため,特異のヤコビアンになる系では問題があるかもしれない.構造行列法ならばこのような場合でも使えるかもしれないが,大きい系では計算複雑度が大きくなる可能性がある.
構造行列法
構造行列アルゴリズムはPantelidesアルゴリズムの代りとなる.構造行列法はUnger [UKM95]とChowdhary et al. [CKL04]の研究に従っている.Pantelidesアルゴリズムのようなグラフベースのアルゴリズムは指数減少法を実行するのに走査に依存するが,特定の系では変数の打消しがある場合があるということを考慮しない.そのため,アルゴリズムは系の指数を少なく見積ることになる.微分代数方程式が指数0あるいは1の系に正しく簡約されないならば,数値積分は失敗するか不正確な結果を出す可能性がある.
Pantelides法で考慮されない変数打消しの例として,次の微分代数方程式を考える.
指数減少法を実行する最初のステップとして,2つ目の方程式を1度微分すると,以下の新しい系が得られる.
Pantelides法は最初の微分の後に変数 ![]() の導関数と走査を見付けるので,そこで中断する.最初の微分の後すべての導関数が見付かるので,Pantelides法は系の指数を0と推定する.指数0の系は常微分方程式系と等価である.微分された系の導関数のヤコビアンは以下の
の導関数と走査を見付けるので,そこで中断する.最初の微分の後すべての導関数が見付かるので,Pantelides法は系の指数を0と推定する.指数0の系は常微分方程式系と等価である.微分された系の導関数のヤコビアンは以下の
であり,これは明らかに特異行列である.代入すると,微分された系は次と等価であることが分かる.
これは,常微分方程式系を得るためには,2つ目の方程式に2回目の微分を行う必要があることを意味している.これで最終的に以下の系が得られる.
この系は導関数に非特異ヤコビアンを持つ.これは正確に指数0の系になっており,これから常微分方程式系を構成することができる.2回の微分が必要だったので,この系の実際の指数は1ではなく2である.
Pantelides法と異なり,構造行列法は線形項に関連する打消しすべてを考慮する.この方法のステップは,一階の系として記述された振り子の例(2)を使って示すことができる.
まず2つの行列![]() および
および![]() が構築される.これらはそれぞれ導関数
が構築される.これらはそれぞれ導関数![]() と変数
と変数![]() に関連付けられた接続行列である.行列
に関連付けられた接続行列である.行列![]() は以下で与えられる.
は以下で与えられる.
上の行列の項目として![]() を含むものがある.
を含むものがある.![]() は方程式の変数(行)が非線形の方程式で表示されていることを示すプレースホルダとして使われている.2つ目の方程式では,項
は方程式の変数(行)が非線形の方程式で表示されていることを示すプレースホルダとして使われている.2つ目の方程式では,項 ![]() と
と ![]() は積として現れている.それゆえ,2行目の最初と最後の列に
は積として現れている.それゆえ,2行目の最初と最後の列に![]() の印がついているのである.
の印がついているのである.
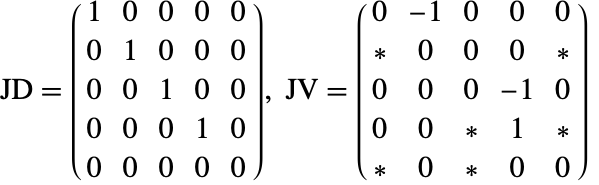
行列が構築されると,その目的は微分代数方程式系を常微分方程式系に変換することになる.そのためには,行列![]() は完全階数でなければならない.これを実現するために,まず微分する必要のある方程式が見付けられる.この場合は最後の方程式である.微分の後,構造行列は次のようになる.
は完全階数でなければならない.これを実現するために,まず微分する必要のある方程式が見付けられる.この場合は最後の方程式である.微分の後,構造行列は次のようになる.
行列![]() の最後の行は微分したために変化した.これをもっとはっきりと見るために,(3)の最後の方程式を考える.方程式を微分すると
の最後の行は微分したために変化した.これをもっとはっきりと見るために,(3)の最後の方程式を考える.方程式を微分すると![]() が得られる.これで項
が得られる.これで項 ![]() が方程式に存在するようになり,非線形で表されている.したがって,導関数に関連付けられた接続行列の行は
が方程式に存在するようになり,非線形で表されている.したがって,導関数に関連付けられた接続行列の行は![]() であり,変数に関連付けられた接続行列の行は
であり,変数に関連付けられた接続行列の行は![]() となる.
となる.
次のステップでは,行列![]() に対して,ガウス消去法の形式での行列因子分解が関わる.
に対して,ガウス消去法の形式での行列因子分解が関わる.![]() の最終行の要素は,行1と3を使うことで消去できる.この消去は行列
の最終行の要素は,行1と3を使うことで消去できる.この消去は行列![]() の行にも影響を及ぼす.
の行にも影響を及ぼす.![]() の最初の行に
の最初の行に![]() を掛け,それに最後の行を代入すると次が得られる.
を掛け,それに最後の行を代入すると次が得られる.
行列![]() はまだ階数落ちであり,上記のステップを再び繰り返さなければならない.2回目の繰返しで以下の系が得られる.
はまだ階数落ちであり,上記のステップを再び繰り返さなければならない.2回目の繰返しで以下の系が得られる.
行列![]() はこれで完全階数の行列になったので,ここで反復を終了する.
はこれで完全階数の行列になったので,ここで反復を終了する.![]() の完全階数行列を得るために3回の反復が必要であったので,この系の指数は3である.Pantelides法とは異なり,構造行列法は接続行列に明示的に作用する.
の完全階数行列を得るために3回の反復が必要であったので,この系の指数は3である.Pantelides法とは異なり,構造行列法は接続行列に明示的に作用する.
次の例ではPantelides法よりも構造行列法が優れている点,および両者の差を示す.次の線形系を考える.
これが失敗するのは,特異のヤコビ行列があるためである.微分代数方程式の指数が1より大きい場合,メッセージNDSolve::nderrあるいはNDSolve::ndcfが出力されるのは珍しくない.
厳密解は ![]() と
と ![]() である.厳密解と数値解を比較すると,計算された解が非常に正確だということが分かる.
である.厳密解と数値解を比較すると,計算された解が非常に正確だということが分かる.
系の指数を過小/過大評価した際の影響を考えるため,以下の線形系を考える.
すべての変数の厳密解は![]() である.これは指数4の系である.Pantelides法は指数を2だと推定している.
である.これは指数4の系である.Pantelides法は指数を2だと推定している.
どちらの指数減少法を使ったらよいかを決めるためにNDSolveが実行するテストがある.この場合,オプションAutomaticを使うと,NDSolveは構造行列法を選ぶ.
もし,この系が指数0として扱われるよう強制されるなら,積分を実行することができる.しかし指数の推定が不正確ではない場合,解は全く異なる多様体について計算されるので,結果は大きくずれる可能性がある.
この問題の厳密解は既知なので,数値解と厳密解の違いを見るのが望ましい.
系の指数を低く見積ったため,必要な微分が実行されず,解は誤った多様体上で近似される.一方,構造行列法は系の指数を正しく見付けることができる.
構造行列法は,このような系をずっとうまく扱う.しかし,打消しに対して支払う代償もあることに注意することが大切である.構造行列法は,Pantelidesアルゴリズムと比べると格段の計算オーバーヘッドを有する行列の生成,維持,操作に依存する.したがってこのアルゴリズムは小規模から中規模の問題にのみ適している.
制約法
ダミー導関数
ダミー導関数の目的は,もとの方程式と指数減少法で微分された方程式を組み合せた系が過剰決定系にならないように代数的変数を導入することである.
振り子の系(2)を再び見てみる.
この例では,"ConstraintMethod"->"DummyDerivatives"が強調のために含まれているが,ダミー導関数はデフォルトなので実際には必要ない.
MattsonとSöderlindのダミー導関数法の考え方[MS93]は,導関数を表す新しい変数を導入することで,過剰決定系を得ることなく制約方程式を再び導入することができるようにすることである.
系(2)に対して指数減少された方程式を思い出してみる.
ここでは,3つ目の方程式からとその最初の導関数からの2つの制約条件がある.
![]() と
と ![]() をそれぞれ
をそれぞれ ![]() ,
,![]() に置き換わる代数的変数とする.制約条件が含まれると,これらの変数の系全体は以下で与えられる.
に置き換わる代数的変数とする.制約条件が含まれると,これらの変数の系全体は以下で与えられる.
一般にアルゴリズムはどの指数減少された微分代数方程式にも適用することができるが,系を積分する間に,ソルバが特異性に遭遇する可能性がある.
上の系は ![]() のときに特異になるので,積分を終了することができない.
のときに特異になるので,積分を終了することができない.
このプロットから,![]() が0に近付くとNDSolveが動かなくなることが分かる.
が0に近付くとNDSolveが動かなくなることが分かる.![]() が0のとき,いくつかの項がなくなり,接続行列は特異になり,非零の対角要素は見付からなくなる.そのため,ダミー導関数の系は実質的に
が0のとき,いくつかの項がなくなり,接続行列は特異になり,非零の対角要素は見付からなくなる.そのため,ダミー導関数の系は実質的に![]() を通過する解に沿って
を通過する解に沿って![]() の指数を持つ.
の指数を持つ.
ダミー導関数の別の置換,つまり ![]() と
と ![]() を
を ![]() と
と ![]() で置き換えることを考えてみる.この置換を持つ系は
で置き換えることを考えてみる.この置換を持つ系は ![]() で特異になる.
で特異になる.
この場合,![]() が0から離れているときは
が0から離れているときは ![]() と
と ![]() を
を ![]() と
と ![]() で置き換えるような動的状態選択を使い,
で置き換えるような動的状態選択を使い,![]() が小さすぎるようになったら
が小さすぎるようになったら ![]() と
と ![]() の代りに
の代りに ![]() と
と ![]() を使って動的にこの系に切り換えるようにするとよい.NDSolveは必要に応じて,ダミー導関数を使った動的状態選択を扱う状態置換規則で自動的にWhenEventを使う.動的状態選択の詳細はこのチュートリアルでは触れない.詳細はMattsonとSoderlindの論文[MS93]を参照のこと.
を使って動的にこの系に切り換えるようにするとよい.NDSolveは必要に応じて,ダミー導関数を使った動的状態選択を扱う状態置換規則で自動的にWhenEventを使う.動的状態選択の詳細はこのチュートリアルでは触れない.詳細はMattsonとSoderlindの論文[MS93]を参照のこと.
投影法
ダミー導関数を使う以外の方法として指数を0に減少させて常微分方程式系を得て,もとの制約条件が確実に満足するよう,投影法を使うというものがある.
振り子の系(2)では,系の指数は3である.つまりすべての変数に対する常微分方程式を得るために,最初と2番目の方程式が1回ずつ微分され,3つ目の方程式は3回微分されなければならないということである.この結果,以下が得られる.
これは導関数 ![]() ,
,![]() ,
,![]() について解くことができる(NDSolveは系を自動的に一階まで簡約する).
について解くことができる(NDSolveは系を自動的に一階まで簡約する).
系の力学を正確に表現するためには,最初の ![]() 回微分された方程式も考慮に入れる必要がある.これらの方程式は下の通りである.
回微分された方程式も考慮に入れる必要がある.これらの方程式は下の通りである.
これらの方程式は各時間刻みで満足しなければならない不変方程式として扱われる.常微分方程式はこれらの方程式を微分することにより導出されたので,制約条件は常微分方程式と矛盾のないことが保障されており,制約条件を不定量として"Projection"時間積分メソッドを使ってこの系を解くことができる.
これはNDSolveに組み込まれている指数減少法を直接使って自動的に行うことができる.
このメソッドでは,もとの制約条件はオプションPrecisionGoalとAccuracyGoalによって指定されたNDSolveの局所的許容誤差まで満足する.
この系には満足しなければならない不変量がまだ他にある.そのうちの一つは![]() で表すことができるエネルギー保存である.投影法は時間刻みの最後だけで投影するので,比較をするのに最も適している.
で表すことができるエネルギー保存である.投影法は時間刻みの最後だけで投影するので,比較をするのに最も適している.
偏微分代数方程式の指数減少
この系では2番目の偏微分方程式には,どの変数に対しても時間導関数要素が含まれていない.したがって,結果となる質量行列は特異行列となり,系は指数1を持つため,NDSolveはこの系を線の方法で解くことはできない.この系の指数を減少させるためには,上の系は次のような行列ベクトル形式で表される.
項 ![]() は空間導関数を離散化することで得られた行列を,項
は空間導関数を離散化することで得られた行列を,項 ![]() は変数
は変数![]() を離散空間区間
を離散空間区間 ![]() で離散化することで得られたベクトルを表す.上記の指数減少法を使って新しい系に指数減少を施す.指数減少された結果の系は以下の通りである.
で離散化することで得られたベクトルを表す.上記の指数減少法を使って新しい系に指数減少を施す.指数減少された結果の系は以下の通りである.
結果となる系はNDSolveで利用できる従来の方法を使って解くことができる.
定数初期条件に基づいた空間グリッドのデフォルトスペースでは,解が時間に伴って生成する変形を扱うには不十分であるため,空間離散には200個の点が使われたことに注目のこと.
指数減少法は時間導関数で実行されるので新しい境界条件は必要なく,系に加える必要もないという点に注意する.しかし,偏微分代数方程式が高階ならば,追加の初期条件が必要になる場合がある.
微分代数方程式の矛盾のない初期化
で表すことができる.これには微分方程式と代数的制約条件を含むことがある.![]() の解を得るためには,積分を開始するための
の解を得るためには,積分を開始するための ![]() および
および ![]() の矛盾のない初期条件集合が必要である.一貫性に対して必要な条件は初期条件が
の矛盾のない初期条件集合が必要である.一貫性に対して必要な条件は初期条件が![]() を満足するということである.しかし,この条件はだけでは十分ではない.もとの方程式を微分すると,また初期条件により満足される必要のある新しい方程式ができるだけだからである.したがって,必要なことは,必要となる矛盾のない条件すべてを満足する初期条件を見付けることである.矛盾のない初期条件を見付けるという問題は,微分代数方程式系を解く上で最も難しい部分の一つであり得る.
を満足するということである.しかし,この条件はだけでは十分ではない.もとの方程式を微分すると,また初期条件により満足される必要のある新しい方程式ができるだけだからである.したがって,必要なことは,必要となる矛盾のない条件すべてを満足する初期条件を見付けることである.矛盾のない初期条件を見付けるという問題は,微分代数方程式系を解く上で最も難しい部分の一つであり得る.
微分代数方程式系は ![]() についての導関数を持つ.これが意味するのは,この問題を一意に解くためには,
についての導関数を持つ.これが意味するのは,この問題を一意に解くためには,![]() に対する初期条件を指定しなければならないということである.しかし,矛盾のない一意の初期条件集合があるため,変数の初期条件を任意に指定することはできない.代数方程式を1回微分すると
に対する初期条件を指定しなければならないということである.しかし,矛盾のない一意の初期条件集合があるため,変数の初期条件を任意に指定することはできない.代数方程式を1回微分すると ![]() が得られる.これを2つ目の方程式に代入すると
が得られる.これを2つ目の方程式に代入すると ![]() の解が得られる.
の解が得られる.![]() を微分して最初の方程式に代入すると
を微分して最初の方程式に代入すると ![]() の解が得られる.これは,この微分代数方程式系の解が決まっているため初期条件も決まっており,
の解が得られる.これは,この微分代数方程式系の解が決まっているため初期条件も決まっており,![]() に対する矛盾のない初期条件の唯一の集合は
に対する矛盾のない初期条件の唯一の集合は ![]() であることを意味する.初期条件の制約条件は一般に明らかではないので,矛盾のない初期条件を見付けるという問題が非常に困難になるのである.
であることを意味する.初期条件の制約条件は一般に明らかではないので,矛盾のない初期条件を見付けるという問題が非常に困難になるのである.
場合によっては,微分代数方程式問題の矛盾のない初期化だけを求めて,解は後で計算することもあろう.これをNDSolveで行う場合は,時間積分の数点を初期条件が指定されている時間と同じにすることで実行できる.このようなステップは,完全な積分を実行する必要がなく,初期条件だけを調べたいときに便利である.
NDSolveは微分代数方程式の初期化にいくつかの方法を提供する.メソッド m はMethod->{"DAEInitialization"->m}を使って指定することができる.
| Automatic | 使用するメソッドを自動的に決定する |
| "Collocation" | 選点法を使う.このアルゴリズムは指数の高い系の初期化に使うことができる |
| "QR" | 指数1の系にQR分解ベースのアルゴリズムを使う |
| "BLT" | 指数1の系にブロック下三角アプローチを使う |
選点法は残差のブラックボックスとして微分代数方程式系を扱うよう設計されており,初期化の点付近の小さい区間上で残差を満足するという目的と達成しようと試みる.この機能により,高指数の系の初期化を扱うためにこのメソッドを使うことができる.しかし,アルゴリズムは微分代数方程式系を分析しないので,系の構造は計算の効率性のためにはつかない.このためこのアルゴリズムは他の方法より遅いのである.
QR法とBLT法は,特に指数1と指数0の系に使うために設計されている.QRメソッドは変数とその導関数の初期条件が反復的に計算されるよう,2つの分離した部分系を生成するために導関数のヤコビアンを分解することに依存する.これによりこのメソッドは非常に効率よくロバストになっている.
BLT法は微分代数方程式系の構造を検査することに依存しており,もとの系を多数の小さい部分系に分割して その各々が効率よく解けるようにする.このメソッドは全体の系と比較して,ずっと小さいヤコビ行列を扱うことになり,そのため大規模の系には計算的に効率がよい.
以下のセクションでは,NDSolveが異なるアルゴリズムを使ってどのように代数微分方程式の矛盾のない初期条件を得るかを説明する.
選点法
として展開することを利用するものである.![]() と
と ![]() を求めるために,
を求めるために,![]() が
が ![]() 個の選ばれた点
個の選ばれた点 ![]() において満足するという条件を実行しようとする.これを行うために,陰的な微分代数方程式は,
において満足するという条件を実行しようとする.これを行うために,陰的な微分代数方程式は,
として線形化される.ここで ![]() と
と ![]() はそれぞれ
はそれぞれ ![]() と
と ![]() に関する
に関する ![]() のヤコビアンを表す.
のヤコビアンを表す.
時間内にこの線形化を ![]() 個の選点に適用すると,係数
個の選点に適用すると,係数 ![]() に対する線形方程式系が得られる.これはニュートン法を使って反復的に解かれる.
に対する線形方程式系が得られる.これはニュートン法を使って反復的に解かれる.
ここで ![]() は直線探索法を使って得られる.
は直線探索法を使って得られる.![]() 個の係数と
個の係数と ![]() 個の選点がある場合,(5)の
個の選点がある場合,(5)の ![]() ×
×![]() の線形方程式系を扱うことになる.
の線形方程式系を扱うことになる.
指数減少を行っていない高指数の系の場合,NDSolveは自動的に選点アルゴリズムを使って系を初期化しようとする.振り子の系(2)を考えてみる.
系の積分を開始するためには,![]() の初期条件が分かっていなければならない.このような系の場合,
の初期条件が分かっていなければならない.このような系の場合,![]() はある物理的特性を表し,合理的な値を割り当てることができる.しかし
はある物理的特性を表し,合理的な値を割り当てることができる.しかし ![]() の値は見付けやすくはないかもしれない.ここで適切な値を決めるのに,NDSolveを使うことができる.
の値は見付けやすくはないかもしれない.ここで適切な値を決めるのに,NDSolveを使うことができる.
部分的な初期条件だけが与えられると,アルゴリズムが必要な初期条件すべてを正しく計算しているのに注目のこと.
選点法のデフォルト設定は,多様な系の初期化を扱うよう選ばれているが,場合によっては矛盾のない初期化を見付けるために設定を変更する必要がある.アルゴリズムを調整するのには以下のオプションが使える.
選点法のオプション名
|
デフォルト値
| |
| "CollocationDirection" | Automatic | 選点が置かれる方向を選ぶ.可能な値は"Forward","Backward","Centered","Automatic"である |
| "CollocationPoints" | Automatic | 使用される選点の数.サブオプションの"ExtraCollocationPoints"を使うと,近似の順序を固定したまま格子点が加わる |
| "CollocationRange" | Automatic | 選点が分布する範囲 |
| "DefaultStartingValue" | Automatic | 非線形の反復における指定されていない要素に使用する初期値.可能な値は1つの要素の値 ig/{ig},あるいは2つの数のリスト{ig1,ig2}である.ここで ig1,ig2はそれぞれ変数の初期値とその導関数である |
| "MaxIterations" | 100 | 実行される繰返しの最大回数 |
次のセクションでは,これらのオプションを詳しく説明し,これらがどのような状況で矛盾のない初期条件を見付けるのに役立つかを示す.
選点の方向
初期化を実行するためには,選点の集合が選ばれる.点はオプション"Centered","Forward","Backward"を使うことで,関心点の両側,前,後ろのどこに置くこともできる.次の表はこれらのオプションを選んだときの効果を示すものである.
上記の項 ![]() は初期条件が計算される時間を指している.項
は初期条件が計算される時間を指している.項 ![]() はオフセット値である.デフォルトでは,NDSolveは自動的に選点法を実行する方向を選択する.
はオフセット値である.デフォルトでは,NDSolveは自動的に選点法を実行する方向を選択する.
NDSolveは"CollocationDirection"のオプションを自動的に設定する.
"Centered"の"CollocationDirection"を適用すると,解は発散する.
しかし,"Forward"か"Backward"の方向を使うと不連続の導関数を避けることで,正しい収束が得られる.
ほとんどの場合,NDSolveは方向がどうあるべきかを自動的に決定する.しかし,特定の方向に不連続性がある可能性があることが分かっているならば,この設定を使ってそれを避けることができる.これがNDSolveの計算時間を削減する助けとなる.
選点
オプション"CollocationPoints"は,(5)で示されるように,級数近似(4)で使用される選点の数 ![]() を指定する.選点によって,(4)の級数の次数
を指定する.選点によって,(4)の級数の次数 ![]() が決まる.級数の次数は
が決まる.級数の次数は ![]() である.選点は選点範囲上に分布したチェビシェフ点である.
である.選点は選点範囲上に分布したチェビシェフ点である.
"CollocationPoints"の働きを見るために,次の指数3の例題を考える.
前の微分代数方程式の解は,解析的に求められる.矛盾のない厳密な初期条件は以下の通りである.
選点は手動で設定することができる."CollocationPoints"->2という設定は,(4)の設定 ![]() と等価である.つまり,解は定数と線形の基底関数を使って近似されるということである.
と等価である.つまり,解は定数と線形の基底関数を使って近似されるということである.
たとえ反復が収束しても,結果は矛盾のない正しい初期条件ではない.この結果は指定された方程式を十分満足しているので,メッセージは生成されない.
高指数の方程式では矛盾のない初期条件は微分された系にも使えることを思い出してほしい.
選点の数を増やし高階の基底関数を許可することで,アルゴリズムは想定された結果に収束することができる.
近似の次数 ![]() は選点
は選点 ![]() により決まるので,(4)で得られた結果の線形化された系は平方行列になり,線形方程式の結果の系はLinearSolveを使って解くことができる.しかし,結果の線形系が悪条件であったり特異であったりする可能性もある.そのような系は高感度といわれ,負担邸名反復となり得る.この問題を解決するためには,多くの場合LeastSquaresを使って方程式の過剰決定系を解くことが望ましい.
により決まるので,(4)で得られた結果の線形化された系は平方行列になり,線形方程式の結果の系はLinearSolveを使って解くことができる.しかし,結果の線形系が悪条件であったり特異であったりする可能性もある.そのような系は高感度といわれ,負担邸名反復となり得る.この問題を解決するためには,多くの場合LeastSquaresを使って方程式の過剰決定系を解くことが望ましい.
サブオプションの"ExtraCollocationPoints"を使うと,級数近似の次数は(4)の ![]() と同じままだが,(5)における
と同じままだが,(5)における ![]() の値は
の値は ![]() (
(![]() は追加の選点)に修正される.それゆえ,これは(5)の方程式の過剰決定系になる.これは最小二乗法を使って解くことができる.
は追加の選点)に修正される.それゆえ,これは(5)の方程式の過剰決定系になる.これは最小二乗法を使って解くことができる.
選点の範囲
指数減少を行っていない非常に高指数の系の場合,選点法を実行する範囲の指定の他,ずっと高い選点の次数を使うことが必要かもしれない.デフォルトでは,選点の範囲は作業精度と,展開で使用される基底関数に基づいて計算される.
通常,系の指数より高次の近似を使う必要がある.これは指数6の系なので,(4)の高次近似に依存しなければならない.前のサブセクションで言及した通り,これはオプション"CollocationPoints"を使って実行することができる.
解は見付かるが,矛盾のない厳密な初期条件からの重大なエラーがある.この大きなエラーの原因は,この例題ではデフォルトオプションが近すぎるために目立った数値丸め誤差があるのである.
"CollocationPoints"と"CollocationRange"の間には密接な関係がある.選点範囲は,過剰な丸め誤差を避け,高精度の計算を可能にするために選点の数に基づいて計算される.明示的に指定されていない限り, "CollocationRange"は![]() として計算される.ここで
として計算される.ここで ![]() はWorkingPrecisionオプションの設定であり,
はWorkingPrecisionオプションの設定であり,![]() は"CollocationPoints"メソッドオプションの設定である.
は"CollocationPoints"メソッドオプションの設定である.
初期条件の指定
常微分方程式と微分代数方程式の主な違いの一つに,常微分方程式系を積分するためには,すべての変数に対する初期条件を与えなければならないというものがある.その一方,微分代数方程式では,これらの初期条件のいくつかは固定されており,系により直接計算されなければならない.詳しく見るために,以下の常微分方程式を考える.
上記の系に対して,初期条件は任意に指定することができる.これで同じ系の修正を以下のように考えることができる.
この系は微分代数方程式であるが,力学は常微分方程式系と同じである.大きな違いは,初期条件 ![]() と
と ![]() は固定されていないが代数方程式によって決定されるということである.
は固定されていないが代数方程式によって決定されるということである.
上の例はどの変数を固定するかについての決定ができるほど簡単で,初期条件は手動で計算される.しかし,慶賀もっと複雑で大きくなると,別のツールに依存する必要がある.
ある場合,初期条件は方程式系によって完全に決定される.この場合を例示するために,次の線形代数微分方程式系を考える.
通常,どの条件が固定されておりどの条件が自由であるかを知ることは不可能であるということに注意しなければならない.正しい初期条件および初期条件の桁数を察する方法の一つとして,初期条件なしで微分代数方程式を直接NDSolveに入れ,メソッド"DAEInitialization"のオプションを操作するというものがある.
一階の系として表される振り子の系(2)を考える.系の状態を一意に定義するためには,2つの初期条件だけが必要である.
まず,この微分代数方程式系に対して与えられる初期条件がない場合を考える.デフォルトでは,最初の推定は指定されていないすべての変数に対して1が取られる.指数減少が実行されていないので,NDSolveは自動的に選点法を選んだ.
アルゴリズムが無限数の可能な集合から可能な初期条件集合を一つ見付けることができたことが分かる.この時点で,初期の推定に非常に高感度である.また,反復の収束は保障されないことも言っておかなければならない.
最初の推定は選点方のオプション"DefaultStartingValue"を使って変更することができる.初期の推定-1が使われると,有効な解の異なる集合が見付かる.
先に述べたように,2つの初期条件は系の状態を固定するのに十分である.振り子の場合,値 ![]() と
と ![]() で系が固定されている.
で系が固定されている.
状態が本当に固定されていると,理論的には系は最初の推定に対して感度が低くなる.
ある系では,初期条件の計算は初期推定に敏感である.それを示すために以下の系を考える.
x2[t]0のこの問題では,一般解は{x1[t]x1[0]+t2/2,x2[t]0,x3[t]t}であり,解を決定するために x1[0]を与えることが必要である.初期推定値としてデフォルト値の1を使うことで,アルゴリズムは指定された初期条件を使うよう強制される.
これは,状態 ![]() に対するデフォルトの初期推定が1であるために起こる.ニュートン反復の間に,2つ目の方程式は完全に満足され,その結果反復は発散するので,系は特異になる.完全に失敗するのを避けるため,このアルゴリズムは
に対するデフォルトの初期推定が1であるために起こる.ニュートン反復の間に,2つ目の方程式は完全に満足され,その結果反復は発散するので,系は特異になる.完全に失敗するのを避けるため,このアルゴリズムは ![]() の指定された条件を修正するよう強制される.
の指定された条件を修正するよう強制される.
この動作を避けるためによりよい初期推定値を与えることができる.初期推定値に-1を使うと,反復は想定された矛盾のない初期状態に収束する.
QR法
QR分解はShampineの研究[S02]に基づいている.このアルゴリズムは指数1および指数0の系を意図したものである.このアルゴリズムは効率的なQR分解法を利用して系の変数とその導関数を分離する.そのようにすることにおいて,各反復ステップで1つの系の解が2つの小さな方程式系に分解される.![]() 個の変数を持つ微分代数方程式系では,選点法が使われたら大きさ
個の変数を持つ微分代数方程式系では,選点法が使われたら大きさ ![]() の行列であるのに対し,QR法は最大で大きさ
の行列であるのに対し,QR法は最大で大きさ ![]() の行列を扱う必要がある.ほとんどの場合,このアルゴリズムは
の行列を扱う必要がある.ほとんどの場合,このアルゴリズムは ![]() よりずっと小さい行列を扱う必要しかない.このことで,このメソッドは非常に大きい系を扱うのに非常に効率的なものとなっている.このセクションでは,もとになっているアルゴリズムを簡単に説明する.
よりずっと小さい行列を扱う必要しかない.このことで,このメソッドは非常に大きい系を扱うのに非常に効率的なものとなっている.このセクションでは,もとになっているアルゴリズムを簡単に説明する.
形式 ![]() の指数が減少した系がある場合,まずそれを初期推定値
の指数が減少した系がある場合,まずそれを初期推定値 ![]() および
および ![]() について
について
として線形化する.QR分解は ![]() となるようにヤコビ行列
となるようにヤコビ行列 ![]() に施される.ここで
に施される.ここで ![]() は直交行列,
は直交行列,![]() は上三角行列,
は上三角行列,![]() は置換行列を表す.微分代数方程式の場合,行列
は置換行列を表す.微分代数方程式の場合,行列 ![]() は完全行階数を持たない.行列
は完全行階数を持たない.行列 ![]() の階数により,線形化された系は以下のように書くことができる.
の階数により,線形化された系は以下のように書くことができる.
一旦要素が見付かると,変換された変数は置換行列を使ってもとの形式に戻される.このプロセスは収束まで繰り返される.
QR法は,メソッド"DAEInitialization"のMethod->{"DAEInitialization"->{"QR",qropts}}(qropts はQR法のオプション)を使って呼び出すことができる.
| "DefaultStartingValue" | Automatic | 非線形反復で指定されていない成分の初期値.可能な値は1要素の値 ig/{ig},2数のリスト{ig1,ig2}である.ここで ig1,ig2はそれぞれ変数とその導関数の初期値である |
| "MaxIterations" | 100 | 最大反復回数 |
これが高指数の微分代数方程式だとすると,系に対して指数減少法を施さなければならない.系の指数が1か0に減少されたら,変数とその導関数すべてが初期化されなければならない.
上記の例題では,矛盾のない初期値の集合となるように初期条件が与えられている.初期条件が矛盾する場合,アルゴリズムは矛盾のない初期値を見付けようと試みる.
オプション"DefaultStartingValue"を指定することで,反復に使われる初期推定値を変更することができる.矛盾のある初期条件の場合,これにより矛盾のない異なる集合が導かれる.
BLT法
BLT法は,指数減少した系をブロック下三角形式に変換して,その系の部分集合を反復的に解いていくことを基本としている.部分集合自体はガウス・ニュートン法で解かれる.指数減少した系を生み出す指数減少アルゴリズムは,すでにブロック下三角形式を持つ傾向にあり,より小さい部分系をそれに対応する小さい行列計算で操作することにより計算の複雑性を減少させるため,この方法は便利なことがある.また,このアルゴリズムは初期条件の矛盾を検証して修正を試みる.
BLT法はメソッド"DAEInitialization"でMethod->{"DAEInitialization"->{"BLT",bltopts}}を使うことで呼び出すことができる.ここで bltopts はBLT法のオプションである.
| "DefaultStartingValue" | Automatic | 非線形の反復において指定されていない成分の初期値.可能な値は1要素の値 ig/{ig}か2数のリスト{ig1,ig2}である.ここで ig1,ig2 はそれぞれ変数とその導関数の初期値である. |
| "MaxIterations" | 100 | 最大反復回数 |
BLT法を使う利点を見るためには,指数減少アルゴリズムが,指数1か0である拡張された方程式系に至るということを認識することが大切である.発熱反応を記述する以下の化学反応系を考えてみる.
下の微分代数方程式は4つの方程式から成っているが,指数減少された系は8つの方程式からできている.指数減少された方程式は以下の通りである.
拡張された系には,ダミーの導関数が含まれたことに注目する.この系をさらに分析すると,系の構造を見ることができる.
上記は,拡張された系が実際には逐次的に解くことができるということを示している.それゆえ,9つの方程式から成る1つの系を持つのではなく,方程式を1つずつ逐次解いていくことができるのである.初期化の見地から,t->0と設定することで変数の初期化が可能になる.
これがBLT法を使う初期化に潜む主要原理である.BLT法は,下三角形式を持つ大きい系を扱うときは特に便利で計算的に効率がよいとされている.
初期条件が矛盾している場合,BLT法は初期条件を適切に修正することができる.しかしながら,BLT法で得られる結果とQR法で得られる結果は異なる可能性があることに注意する必要がある.初期条件が矛盾した振り子の例を考えてみる.
矛盾した初期条件
微分代数方程式系の定式化とその解において最も難しいことに一つに,最初の初期条件が矛盾のないものでなければならないということがある.これは単純に見えるが,高指数の微分代数方程式系では,初期条件も満足しなければならない隠れた条件/方程式に簡単に遭遇する.NDSolveが矛盾した初期条件に遭遇すると,それを修正しようと試みる.
隠れた制約条件と矛盾のある初期条件についての要点を説明するために,振り子の系(2)を考えよう.
最初の場合として,初期条件が系の代数的制約条件に反するときを考える.これは ![]() の初期条件が制約条件
の初期条件が制約条件![]() に常に反するように意図的に設定することで行える.
に常に反するように意図的に設定することで行える.
系がNDSolveに渡されると,NDSolve::ivresというメッセージが生成され初期条件が矛盾していることを表す.その後NDSolveは矛盾した値をその反復の初期推定として使って,矛盾のない初期条件を見付けようとする.
指定された条件が矛盾しているかどうかがはっきりしない場合がある.初期条件は制約条件を満足してるように見えても,隠れた制約条件は満足していないかもしれない.
これらの初期条件は方程式 ![]() を満足するが,暗示的な制約条件
を満足するが,暗示的な制約条件 ![]() を満足することはできない.この制約条件は隠れており指数減少によってのみ見付かるので,明白ではない.選点法は指数減少を実行しないで,もとの方程式に作用する.指数減少した系がなくても,選点法は初期条件の矛盾を検出することができ,それを修正しようと試みる.
を満足することはできない.この制約条件は隠れており指数減少によってのみ見付かるので,明白ではない.選点法は指数減少を実行しないで,もとの方程式に作用する.指数減少した系がなくても,選点法は初期条件の矛盾を検出することができ,それを修正しようと試みる.
イベントを使った微分代数方程式の再初期化
状態の変化が ![]() で起こる,離散変数を持った2つの方程式から成る系を考える.
で起こる,離散変数を持った2つの方程式から成る系を考える.
この例では ![]() と
と ![]() に対する初期条件が与えられている.初期化コードが矛盾のない初期条件
に対する初期条件が与えられている.初期化コードが矛盾のない初期条件 ![]() を自動的に計算する.時間
を自動的に計算する.時間 ![]() で,離散変数は1から2に変更しなければならないというイベントが発生する.
で,離散変数は1から2に変更しなければならないというイベントが発生する.![]() において変数の再初期化が必要になる.変数
において変数の再初期化が必要になる.変数 ![]() は修正された変数と呼ばれる.再初期化中に,以下のようなストラテジーが適用される.
は修正された変数と呼ばれる.再初期化中に,以下のようなストラテジーが適用される.
1. すべての状態変数,離散変数,修正された変数は固定しておく.状態変数の導関数が固定されたら(あるいは変更するよう指定されたら),その変数は変更することができる.
2. ストラテジー1が再初期化に失敗したら,状態変数と修正された変数を固定して,他の変数とその導関数は変更できるようにする.
3. ストラテジー2が失敗したら,修正された変数と,代数微分方程式の導関数を持つ状態変数を固定して,その他すべての変数とその導関数は変更できるようにする.
4. ストラテジー3が失敗したら,修正された変数だけを固定して,状態変数とその導関数はすべて変更できるようにする.
参照されたストラテジーをもとに,時間 ![]() でストラテジー1と2を使うと,
でストラテジー1と2を使うと,![]() ,
,![]() ,
,![]() は変更してはならない.
は変更してはならない.![]() だとすると,これは明らかに代数方程式
だとすると,これは明らかに代数方程式 ![]() に反する.したがって,ストラテジー1と2は失敗に終わる.
に反する.したがって,ストラテジー1と2は失敗に終わる.
ストラテジー3では,導関数を持つ変数は変更してはならない.よって,![]() は
は ![]() とともに固定したままであるが,
とともに固定したままであるが,![]() は変更してもよい.これにより
は変更してもよい.これにより ![]() の値はプロットで示されている(青い線)ように修正される.
の値はプロットで示されている(青い線)ように修正される.
WhenEventは,状態変化を含むイベント動作を同時評価することも逐次評価することもできる.
各状態変化の後,同じイベントでも,微分代数方程式は上のストラテジーを使って再初期化される.そのため,可能ならば,必要な状態変化に対して1つの規則だけを与えた方が効率できである.同じイベント時において実行される複数の状態変化があるときの最後の状態は,異なる可能性がある.なぜなら,各後続の評価と設定で新しい値が使われ,微分代数方程式ではこれらの値は再初期化に依存するかもしれないからである.追加のイベントを含む前の問題を考えてみる.
なぜこの解が上の解とは異なっているかを見るためには,一連の設定を追ってみる必要がある.まず ![]() が2に設定され,微分代数方程式は他の設定を評価する前に再初期化される.再初期化によって
が2に設定され,微分代数方程式は他の設定を評価する前に再初期化される.再初期化によって ![]() の値が2に変わる.そのようにして,上記のストラテジーが残差と矛盾のない解を見付けるからである.2つ目の動作の実行で
の値が2に変わる.そのようにして,上記のストラテジーが残差と矛盾のない解を見付けるからである.2つ目の動作の実行で ![]() が2(
が2(![]() の現行値)に設定されるが,これは残差と矛盾する.したがって
の現行値)に設定されるが,これは残差と矛盾する.したがって ![]() が代数的変数なので,その値は4(
が代数的変数なので,その値は4(![]() )に設定される.最後に
)に設定される.最後に ![]() を
を ![]() に設定すると
に設定すると ![]() が2にリセットされ,新規に設定された代数的変数を修正することを避けるため,
が2にリセットされ,新規に設定された代数的変数を修正することを避けるため, ![]() の値は1にリセットされる.
の値は1にリセットされる.
変化の結果を見る一つの方法は,設定と設定の間にPrintコマンドを入れることである.
規則が1つの場合初期化は1つだけなので,すべての変数が設定されると,与えられる値は矛盾がないものでなければならない.さもないと,再初期化ストラテジーは失敗するか,想定された値を与えないようになる.
ここでは ![]() ,
,![]() ,
,![]() が固定されている.これは非常に厳しい制約条件であり,すべてのストラテジーが失敗する.
が固定されている.これは非常に厳しい制約条件であり,すべてのストラテジーが失敗する.
有効な単独規則内で変数を現行の値に設定すると,同じままであるよう強制することになる.
微分代数方程式の例題
トーラスの問題
これはCampbell & Moore [CM95]からのテスト問題である.微分代数方程式は粒子の動きを3Dで表す.これは3つの位置変数,3つの速度変数,1つの係数を持つ指数3の微分代数方程式である.解多様体は四次元であり,厳密解は以下で与えられる.
タンクからの圧力の解放
これは石油化学工学の動的プロセスを簡約したモデルである.このモデルの詳細は,Hairer et. al. [HLR89]をご参照いただきたい.これは指数2の系である.
非伸縮性スライダークランク
次の例題は制約条件付きの簡単な多体システムである.このシステムは固定面に固定された質量m1のクランク,質量m3のスライダー,質量m2の連結棒で構成されている.このスライダーは水平面でのみ移動が可能である.各部品の質量のため,このシステムの構築中に慣性モーメントを考慮する必要があった.問題の概略は以下に示す通りである.このシステムは2つの角度を使って完全に定義することができる.
スライダクランクメカニズムの状態は2つの角度 ![]() と原点からのスライダの距離
と原点からのスライダの距離 ![]() で完全に表すことができる.
で完全に表すことができる.
運動の方程式は,力を分散し,ニュートンの法則 ![]() と
と ![]() .を適用することによって導かれる.
.を適用することによって導かれる.
接続軸にバネ制振装置を装備したスライダクランク
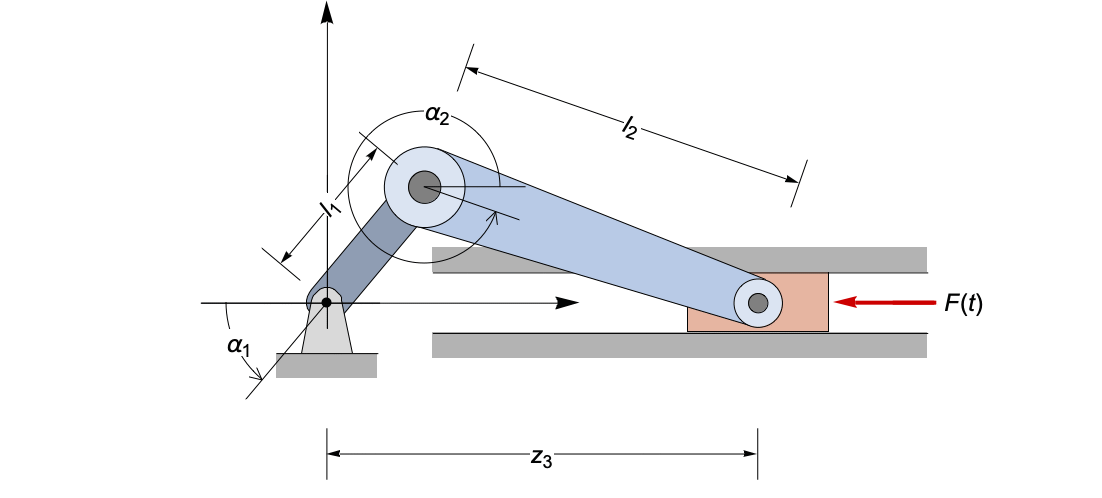
これは簡単なスライダクランク機構の拡張である.クランクと接続軸の間にバネと制振装置を装備する.このばねはクランクの動きの範囲を制約し,制振装置はゆっくりとシステムを安定した状態にする.系の概略は以下の通りである.
スライダクランクメカニズムの状態は2つの角度 ![]() と原点からのスライダの距離
と原点からのスライダの距離 ![]() で完全に記述することができる.
で完全に記述することができる.
運動の方程式は,力を分解し,ニュートンの法則 ![]() と
と ![]() を適用することによって導かれる.
を適用することによって導かれる.
2リンク平面ロボットアーム
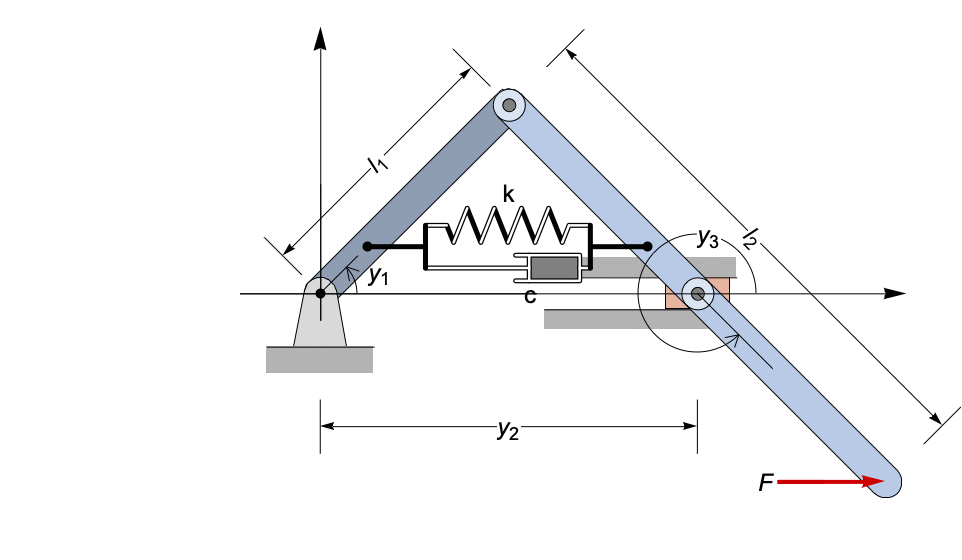
2リンク平面ロボットアームは,無摩擦の制約された機械システムである.このシステムは,2つ目のリンクの一端の軌道が指定されている一方で,最初のリンクの一端が固定されたままとなるようにジョイントで互いに接続された2つのリンクからできている.以下の図はこのシステムの概略である.
このシステムはリンク間の角度を使って完全に定義することができる.このシステムの詳細はAscher et al. [ACPR94]でご覧いただきたい.
運動の方程式は,力を分解しニュートンの法則を適用することで導かれる.微分方程式は角度に対して導かれる.したがって,デカルト座標![]() および
および![]() は,角度で表される.
は,角度で表される.
n 振り子問題
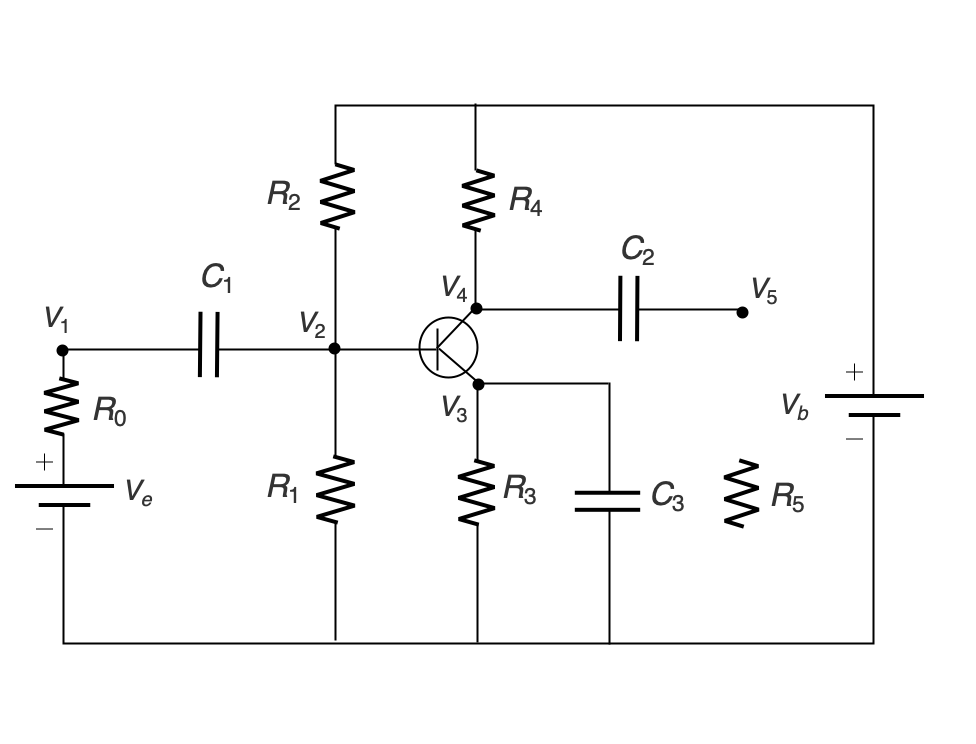
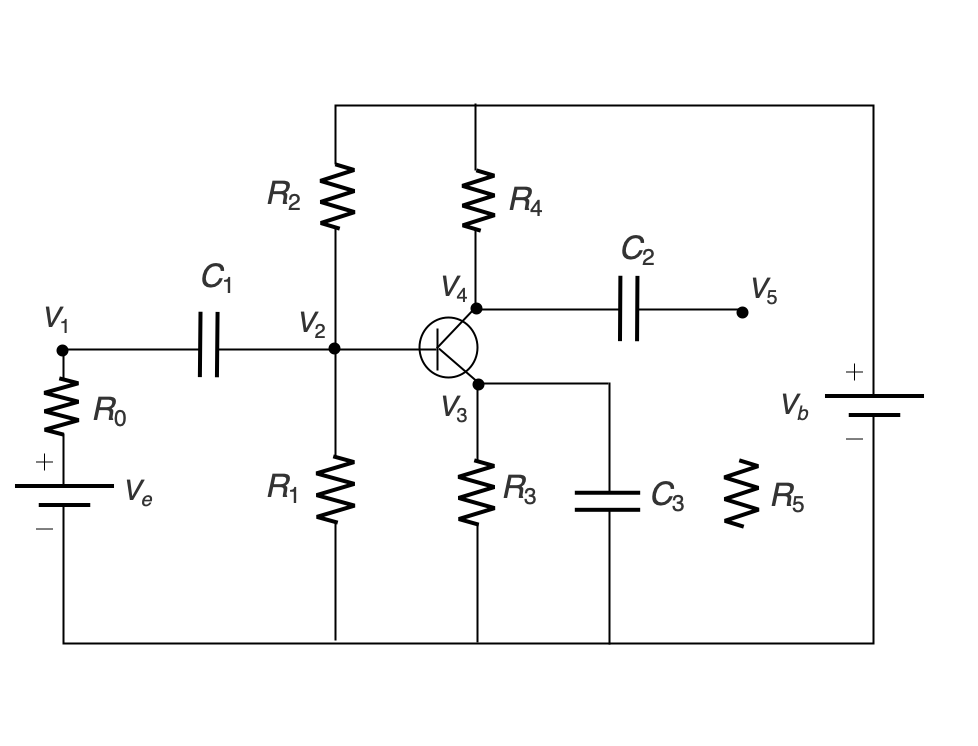
トランジスタ増幅回路
Akzo-Nobelの化学反応
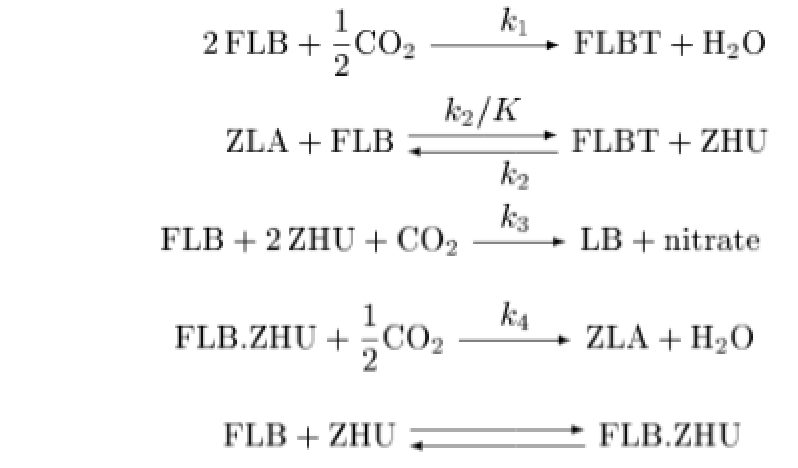
次のシステムは,2つの物質FLBとZHUが混合され,その間常に![]() がシステムに加えられるという科学プロセスを記述している.この化学物質名は架空のものである.このシステムとそれに関連するダイナミクスは[N93]に記載されている.反応方程式は下に示す.それぞれの反応と関連して反応速度があり,指定されている.代数的制約は,FLBとZHU,およびその混合体が一定の関係を保つよう要求している最後の反応から派生している.
がシステムに加えられるという科学プロセスを記述している.この化学物質名は架空のものである.このシステムとそれに関連するダイナミクスは[N93]に記載されている.反応方程式は下に示す.それぞれの反応と関連して反応速度があり,指定されている.代数的制約は,FLBとZHU,およびその混合体が一定の関係を保つよう要求している最後の反応から派生している.
車軸問題
車軸モデルは,でこぼこ道での車軸の動作をシミュレーションするために設計された簡単な多体系である.この系の概略を以下に示す.このモデルは2つの車輪からできている.左の車輪は平坦な面の上を動き,右の車輪はでこぼこの表面上を動くものとされている.でこぼこの表面は正弦曲線としてモデル化される.両方の車輪は,以下に示すように質量の無視できる2つのバネを通して,その動きを車のシャーシに伝達する.車のシャーシは質量Mのバーとしてモデル化される.このモデルの詳細はMazzia et. al. [MM08]で見ることができる.これは指数3の系である.
左側のタイヤは常に平面にあり,右側のタイヤは定期的にでこぼこの上を走る.
タイヤとタイヤの間の距離は,常に固定されたままでなければならず,車のシャーシは常に固定された長さでなければならない.
楕円型偏微分方程式と放物型偏微分方程式の1Dでの結合
次は,非線形の形式で結合された放物型偏微分方程式と楕円型偏微分方程式を解くための合成例題である.偏微分方程式の空間的離散性により,かなり多数の代数的変数を含む系になる.方程式は,系に対して解析的解が存在するように設定される.結合系の詳細は以下で与えられる.
多種の食物網モデル(楕円型偏微分方程式と放物型偏微分方程式の2Dでの結合)
この例は,多種の食物網のモデルである[B86].典型的な捕食被食問題とは異なり,この問題には空間的要素が存在する.捕食被食関係は一連の拡散パラメータを使って2Dの空間領域上で定義される.一般的な結合偏微分方程式は以下で与えられる.
上の系では,最初の ![]() 種が被食者,次の
種が被食者,次の ![]() 種が捕食者である.ここでは
種が捕食者である.ここでは ![]() の特殊な場合が考慮される.つまり,1種の捕食者と1種の被食者がいるということである.空間領域は20×20のメッシュで離散化される.最終的な微分代数方程式系には2×400個の変数があることになる.捕食者の一様分布は最初に指定される.これは矛盾した初期状態になるが,組込みのアルゴリズムで修正される.
の特殊な場合が考慮される.つまり,1種の捕食者と1種の被食者がいるということである.空間領域は20×20のメッシュで離散化される.最終的な微分代数方程式系には2×400個の変数があることになる.捕食者の一様分布は最初に指定される.これは矛盾した初期状態になるが,組込みのアルゴリズムで修正される.
Andrewsの圧搾器メカニズム
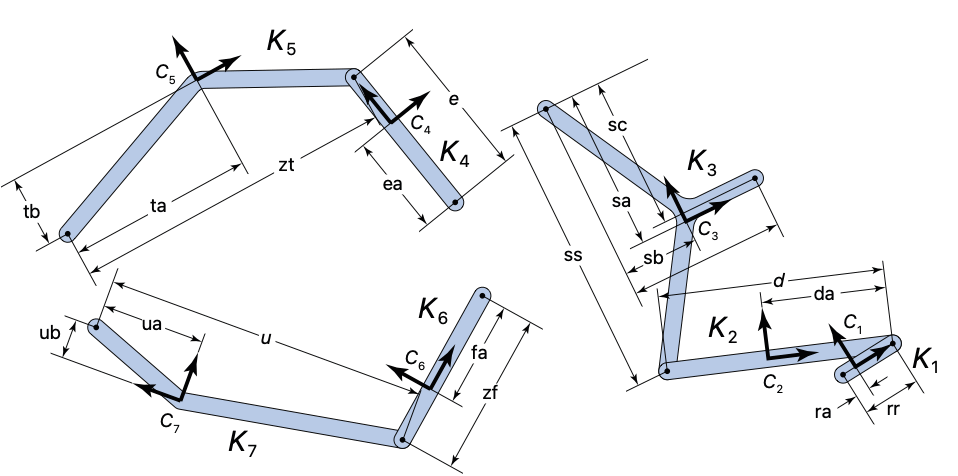
Andrewsの圧搾器メカニズムは7つの異なるリンクを含む多体系である.さまざまなリンクの次元およびその指定は以下にある通りである.この系は7つの角度を使って完全に定義することができる.角度は次の系で q1–q7としてラベル付けされている.また,リンクの次元と接続に関連付けられた6つの代数的制約がある.これにより14次元の指数3の系になる.このシステムの詳細はHairerとWanner[HW96]の論文を参照されたい.
さまざまなリンクに関連付けられた次元は以下に示す通りである.7つのリンクがK1–K7でラベル付けされている.
モデルで使われるパラメータの表記とその説明は,HairerとWannerの論文[HW96]に記載されている.
系の運動は7つの角度を使って定義することができる.この角度はここで ![]() と定義されている.運動の方程式は,形式
と定義されている.運動の方程式は,形式 ![]() の方程式系になるハミルトニアン原理を使って導かれる.ここで
の方程式系になるハミルトニアン原理を使って導かれる.ここで ![]() は質量行列,
は質量行列,![]() は力のベクトル,
は力のベクトル,![]() は制約条件のベクトル,λ はラグランジュの乗数である.
は制約条件のベクトル,λ はラグランジュの乗数である.