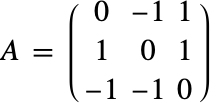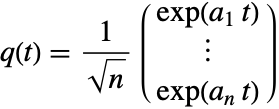NDSolveの"OrthogonalProjection"メソッド

はじめに実装
例題オプションの要約

はじめに

初期値 が与えられている以下の行列微分方程式について考える．

ここで， が成り立ち，解は正規直交性を保存する特性 を持ち，のすべてに対してフルランクを持つと仮定する．

数値的観点から問題となるのは，数値解が直交解のまま維持されるように，直交行列の微分方程式系を数値的に積分する方法である．これには可能な方法がいくつかある．[DRV94]で提案されているひとつのアプローチは，ガウス法等の陰的ルンゲ・クッタ(Runge-Kutta)法を使うことである．この他の方法は[DV99]と[DL01]に記述されている．

ここで取り上げるアプローチは，あらゆる合理的な数値積分法を使い，各積分ステップの最後で投影を使って後処理するというものである．

この実装の重要な特徴は，基本的な積分法はどの組込み数値法でもよく，ユーザ定義のものでも構わないという点である．以下に挙げる例では，基本的な時間刻みに陽的ルンゲ・クッタ法を使っている．しかし，精度を上げる必要があるなら，例えば，適切なMethodオプションを設定するだけで，簡単に外挿法を使うこともできる．

投影

直交行列を得るためには，各数値積分ステップの最後で微分方程式系の近似解行列を変換する必要がある．これは以下のいくつかの方法で実行できる（[DRV94]と[H97]も参照のこと）．

シュルツ反復法

選ばれたアプローチは， のとき直接作用するシュルツ反復法に基づく．これとは対照的に， のニュートン反復法では，先にQR分解をしておく必要がある．

特異値分解に基づく直接計算との比較も参照する．

シュルツ反復法は以下で与えられる．

シュルツ反復法は，の浮動小数点操作を反復する毎に算術操作をカウントするが，行列の乗算が多い[H97]．

実際の実装では，Automatically Tuned Linear Algebra Software [ATLAS00]を使って，特定のアーキテクチャ用に最適化すると共に，LAPACKのGEMMベースlevel 3のBLAS[LAPACK99]を使うことができる．これは，シュルツ反復法の算術操作カウントが，必ずしも観察される計算コストを正確に反映してるわけではないことを意味している． の正規直交性からの逸脱についての境界は，[H89]に記述されている である．シュルツ反復法の比較は，ある許容値 での収束判定条件 を与える．

標準公式

ODEの現在の解の初期値 および1ステップの数値積分法の解 が与えられているとする．また，シュルツ反復法を制御する絶対許容誤差 も決められているとする．

この場合，以下のアルゴリズムを使って実装できる．

ステップ1．と を設定する．

ステップ2． を計算する．

ステップ3．を計算する．

ステップ4． あるいは ならば，を返す．

ステップ5．を設定してステップ2に戻る．

増分公式

NDSolveは補償総和を使って，各積分段階の最後で少数量の を に繰返し加えることによって生じた丸め誤差効果を軽減する[H96]．従って，増分 は基本積分によって返される．

反復投影の適切な直交補正 は，以下のアルゴリズムを使って決定することができる．

ステップ1．と を設定する．

ステップ2．を設定する．

ステップ3． を計算する．

ステップ4．を計算する．

ステップ5． あるいは ならば， を返す．

ステップ6．を設定してステップ2に戻る．

"OrthogonalProjection"では，この修正アルゴリズムが使われている．また，直接法の直交補正がどのように導出できるのかが明確ではないため，直接法よりも反復法を使った方が有利であることを示している．

例題

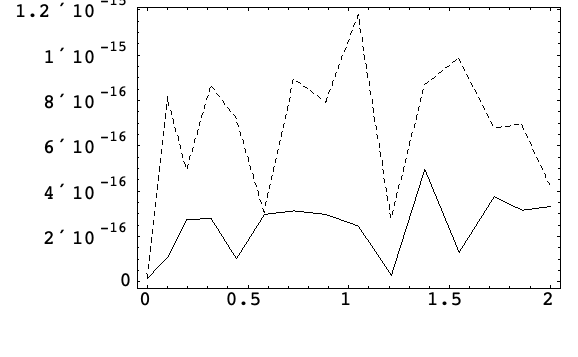
直交誤差測定

行列 のフロベニウス(Frobenius)ノルム を計算する関数は，以下のようにNorm関数で定義することができる：
の直交正規性からの逸脱の上限は，以下の関数を使って測定できる[H97]：
数値積分での直交誤差を視覚化する効用関数を定義する：

正方行列

ここでは，直交群 上の正方行列の微分方程式系の解に関する例を挙げる（[Z98]を参照のこと）．

行列微分方程式系は以下で与えられる．

このとき

であり

である．解は下のように進化する．

の特異値は ，，である．よって， が に近付くにつれ，の特異値のうちの2つが-1に近付く．数値積分は，区間で実行される：
陽的ルンゲ・クッタ(Runge-Kutta)法を使って解を計算する．適切な初期刻み幅とメソッドの次数は自動的に選択される．刻み幅は積分区間内で変化する可能性があり，これは局所的な相対・絶対許容誤差を満足するよう選ばれる．また，メソッドの次数をMethodオプションで指定することもできる：
積分が進むに従って直交誤差（直交多様体からの絶対偏差）を計算する．誤差は数値法の局所精度の次数となる：
これは基本的積分ステップとして陽的ルンゲ・クッタ法を用い，正射影を使って解を計算する．初期刻み幅とメソッドの次数は既出のものと同様であるが，積分における刻み幅のシーケンスは異なるかもしれない：
正射影を使うと，直交誤差はおよそIEEE倍精度の丸め誤差レベルにまで減少する：
増分公式を使うシュルツ反復法では，一般的に直接の特異値分解よりも誤差が小さい：

長方行列

ここでは，正射影の実装がどのように長方行列の微分方程式系にも作用するかを例示する．上述の通り， のときの × 直交行列集合であるStiefel多様体上の常微分方程式が解きたいものとする．

定義　× 直交行列のStiefel多様体とは集合 （ここで）で， は × 単位行列である．

Stiefel多様体上で発展する解は，数値線形代数の特異値問題，動的システムおよび信号処理におけるリアプノフ(Lyapunov)指数の計算等のさまざまな応用分野で見られる．

[DL01]から以下の例を取り上げる．

ここで で のとき，， が成り立つ．

厳密解は以下で与えられる．

を

に正規化すると，が次の 上の弱い歪対称な系を満足するということに従う．

次の例では，系が ，次元 で区間上で解かれる：
これは積分区間で常に評価することのできる厳密解を計算する：
陽的ルンゲ・クッタ法を用いて解を計算する：
積分区間の最後で，要素の絶対大域誤差を計算する：
直交誤差（Stiefel多様体からの偏差）を計算する：
これは基本的な数値積分法として陽的ルンゲ・クッタ法を用いて，正射影を使って解を計算する：
積分区間の最後における要素の絶対大域誤差は，以前とほとんど等しい．これは数値積分で使われた絶対許容誤差と相対許容誤差が同じであるためである：
しかし直交投影法を使うと，Stiefel多様体からの偏差は丸め誤差のレベルに減少する：

実装

メソッド"OrthogonalProjection"の実装には，3つの基本的な要素がある．

オプションの要約

オプション名
デフォルト値
Dimensions{}行列微分系の次元を指定する．
"IterationSafetyFactor"シュルツ反復法(1)の収束判定条件で使う安全率を指定する．
MaxIterationsAutomaticシュルツ反復法(2)で使う最大反復数を指定する．
Method"StiffnessSwitching"数値積分で使うメソッドを指定する．

"OrthogonalProjection"メソッドのオプション