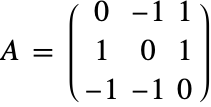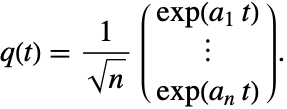NDSolve 的“Projection”方法

引言实现
示例选项总结

引言

考虑该矩阵微分方程：

其中给出初值 . 假设 ，该解具有保持标准正交性的属性，，并且它对于所有 满秩.

从数值的角度来看，一个关键的问题是如何对一个正交矩阵微分系统数值积分，积分的方式使得数值解仍然正交. 有一些可能的策略. 一种方法，在 [DRV94] 中提出，是采用隐式朗格-库塔方法（如高斯方案）. 一些替代的策略在 [DV99] 和 [DL01] 中有描述.         

这里采用的方法是使用任何合理的数值积分方法，然后在每个积分步的末尾使用投影程序进行后处理.

该实现方法的一个重要特点是基本积分方法可以是任何内置的数值计算方法，或者甚至是一个用户定义的过程. 在下面的例子中，一个显式朗格-库塔方法用于基本时间步进（the basic time stepping）. 但是，如果需要更高的精确度，则可以方便的使用一个外推法（ extrapolation method），例如，通过简单地设置适当的 Method 选项.

投影步（Projection Step）

在每个数值积分步的末尾，用户需要转换该微分系统的近似解矩阵以获取一个正交矩阵. 这可以通过一些方式实现（例如，见 [DRV94] 和 [H97]）:

Schulz 迭代

选择的方法基于 Schulz 迭代，它对于 直接适用. 相比之下， 迭代需要先进行 QR 分解.

与基于奇异值分解的直接计算的比较也在这里给出.

Schulz 迭代由下式给出：

Schulz 迭代在每个 浮点运算的迭代中具有一个运算操作，但是具有更丰富的矩阵乘法 [H97].

在一个实际实现中，LAPACK [LAPACK99] 的GEMM-based level 3 BLAS 可以通过自动调谐线性代数软件 [ATLAS00]，与特定体系的优化结合起来使用. 这样的考虑意味着，Schulz 迭代的运算操作数目不一定是观察到的计算代价的准确反映. 从 的标准正交性的偏离的有用的界限在 [H89] 中给出：. 与 Schulz 迭代的比较给出对于一些容差 的终止标准 .

标准公式

假定给出常微分方程的当前解的一个初值 ，以及从一步数值积分方法所得的一个解 . 假定控制Schulz 迭代的一个绝对容差 也预先给定.

下面算法可以用于实现.

第 1 步. 设置 和 .

第 2 步. 计算 .

第 3 步. 计算 .

第 4 步. 如果 或者 , 那么返回 .

第 5 步. 设置 并且跳到第2步.

增量公式

NDSolve 使用赔偿总和来降低由于在每个积分步重复增加小数值 给 产生的舍入误差的效果 [H96]. 因此，增量 由基本积分器返回.

投影迭代的一个合适的正交修正 可以使用下面算法确定.

第 1 步. 设置 和 .

第 2 步. 设置 .

第 3 步. 计算 .

第 4 步. 计算 .

第 5 步. 如果 或者 ，那么返回 .

第 6 步. 设置 并且跳到第 2 步.

该修正算法在 "OrthogonalProjection" 中使用，并且显示了使用迭代算法比使用直接过程的优点，由于一个正交修正如何对直接方法推导并不明显.

示例

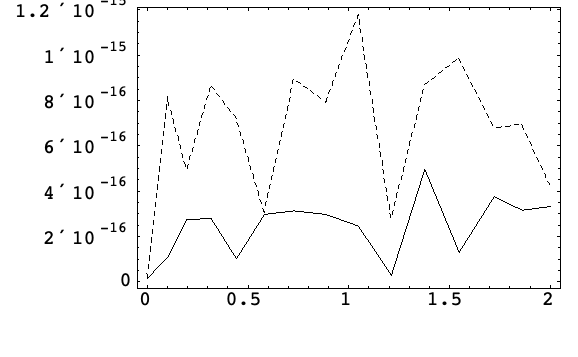
正交误差测量

计算一个矩阵 的Frobenius 范数 的一个函数可以关于下面的 Norm 函数定义：
从 的标准正交性偏离的上界可以使用该函数 [H97] 测量：
这里定义功用函数，用于可视化在一个数值积分中的正交误差：

方形系统（Square Systems）

这个例子涉及一个矩阵微分系统在正交群 上的解（见 [Z98]）.

矩形微分系统由下列式子给出

其中

并且

解的演化为：

的特征值是 , , . 因此，当 接近 时， 的两个特征值接近 -1. 在区间 上执行数值积分：
这里使用显式朗格-库塔方法计算解. 适当的初始步长和方法的阶数被自动选择，并且在积分区间中步长可能有所不同，步长的选择为了满足局部相对和绝对误差容差. 另一方面，方法的阶数可以使用一个 Method 选项指定：
这里当积分进行时，计算正交误差，或者从正交流形的绝对偏差. 该误差是数值方法的局部准确度的阶数：
这里使用用于基本积分步骤的显式朗格-库塔法的正交投影法，计算解. 初始步长和方法的阶数与之前的相同，但是在积分中的步长序列可能有所不同：
利用正交投影法，正交误差被降低为接近IEEE双精度运算中四舍五入的水平：
Schulz 迭代，利用增量公式，一般产生比直接奇异值分解更小的误差：

矩形系统

下面的例子表明正交投影方法的实现对于矩形矩阵微分系统也适用. 正式地表示为，我们感兴趣的是在 Stiefel 流形 上，求解常微分方程，即 × 正交矩阵的集合，其中 .

定义 × 正交矩阵的 Stiefel 流形 是集合 , , 其中 是 × 单位矩阵.

在 Stiefel 流形上演化的解找到许多应用，如在数值线性代数中的特征值问题，动力系统和信号处理的 Lyapunov 指数的计算.

考虑从 [DL01] 中采用的一个例子：

其中 , ，而 并且 .

精确解由下列式子给出：

把 标准化得到：

因此， 满足下列 上的弱斜对称系统：

在下面的例子中，该系统在区间 中被求解，其中 并且维度 ：
这里计算精确解，该解可以在积分区间内被计算：
这里使用显式朗格-库塔方法计算解：
这里计算在每个积分区间末尾的按分量的绝对全局误差：
这里计算正交误差——一个 Stiefel 流形偏差的测量：
这里使用一个正交投影法计算解，该方法使用朗格-库塔方法作为基本的数值积分方案：
在积分区间结尾处的，按分量的绝对全局误差（The componentwise absolute global error）大致与之前的相同，这是因为在数值积分中使用的绝对和相对容差是相同的：
利用正交投影法，但是，Stiefel 流形的偏差降低到四舍五入的水平：

实现

方法 "OrthogonalProjection" 的实现具有三个基本组成部分：

选项总结

选项名
默认值
Dimensions{}指定矩阵微分系统的维度
"IterationSafetyFactor"指定 Schulz 迭代 (1) 的终止标准中所采用的安全因子
MaxIterationsAutomatic指定在 Schulz 迭代 (2)中采用的最大迭代次数
Method"StiffnessSwitching"指定数值积分采用的方法

方法 "OrthogonalProjection" 的选项.