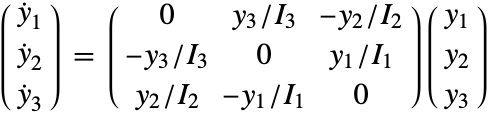WOLFRAM

Wolfram Language & System Documentation Center
Rigid Body Solvers

Rigid Body Solvers

IntroductionMethod Comparison
Manifold Generation and Utility Functions

Introduction

The equations of motion for a free rigid body whose center of mass is at the origin are given by the following Euler equations (see [MR99]).

Two quadratic first integrals of the system are:

The first constraint effectively confines the motion from to a sphere. The second constraint represents the kinetic energy of the system and, in conjunction with the first invariant, effectively confines the motion to ellipsoids on the sphere.

Numerical experiments for various methods are given in [HLW02] and a variety of NDSolve methods will now be compared.

Manifold Generation and Utility Functions

Load some useful packages:
Define Euler's equations for rigid body motion together with the invariants of the system:
The equations of motion evolve as closed curves on the unit sphere. This generates a three-dimensional graphics object to represent the unit sphere:
This function superimposes a solution from NDSolve on a given manifold:
This function plots the various solution components:

Method Comparison

Various integration methods can be used to solve Euler's equations and they each have different associated costs and different dynamical properties.

Adams Multistep Method

Here an Adams method is used to solve the equations of motion:
This shows the solution trajectory by superimposing it on the unit sphere:
The solution appears visually to give a closed curve on the sphere. However, a plot of the error reveals that neither constraint is conserved particularly well:

Euler and Implicit Midpoint Methods

This solves the equations of motion using Euler's method with a specified fixed step size:
This solves the equations of motion using the implicit midpoint method with a specified fixed step size:
This shows the superimposition on the unit sphere of the numerical solution of the equations of motion for Euler's method (left) and the implicit midpoint rule (right):
This shows the components of the numerical solution using Euler's method (left) and the implicit midpoint rule (right):

Orthogonal Projection Method

Here the "OrthogonalProjection" method is used to solve the equations:
Only the orthogonal constraint is conserved so the curve is not closed:
Plotting the error in the invariants against time, it can be seen that the orthogonal projection method conserves only one of the two invariants:

Projection Method

The method "Projection" takes a set of constraints and projects the solution onto a manifold at the end of each integration step.

Generally all the invariants of the problem should be used in the projection; otherwise the numerical solution may actually be qualitatively worse than the unprojected solution.

The following specifies the integration method and defers determination of the constraints until the invocation of NDSolve:

Projecting One Constraint

This projects the first constraint onto the manifold:
Only the first invariant is conserved:
This projects the second constraint onto the manifold:
Only the second invariant is conserved:

Projecting Multiple Constraints

This projects both constraints onto the manifold:
Now both invariants are conserved:

"Splitting" Method

A splitting that yields an efficient explicit integration method was derived independently by McLachlan [M93] and Reich [R93].

Write the flow of an ODE as .

The differential system is split into three components, , , and , each of which is Hamiltonian and can be solved exactly.

The Hamiltonian systems are solved and recombined at each integration step as:

This defines an appropriate splitting into Hamiltonian vector fields:
Here is the differential system for Euler's equations:
Here are the three split vector fields:

Solution

This defines a symmetric second-order splitting method. The coefficients are automatically determined from the structure of the equations and are an extension of the Strang splitting:
This solves the system and graphically displays the solution:
One of the invariants is preserved up to roundoff while the error in the second invariant remains bounded: