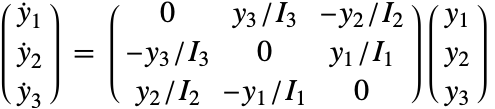剛体ソルバ

はじめに方法の比較
多様体生成および効用関数

はじめに

重心が原点となっている自由剛体の運動方程式は，以下のオイラー方程式で与えられる（[MR99]を参照のこと）．

以下はこの系の第1積分の2つの二次方程式である．

最初の制約条件は，実質的に運動をから球面へ制限する．第2の制約条件は系の運動エネルギーを表し，最初の不変式と連動して，運動を球面の楕円に制限する．

さまざまな方法での数値的な実験は[HLW02]に挙げてある．ここでは，NDSolveのさまざまな用法を比較する．

多様体生成および効用関数

まず，便利なパッケージをいくつかロードする：
剛体運動と系の不変式に対してオイラー方程式を定義する：
運動方程式は単位球上で閉曲線として進化する．これにより，その単位球を表す3Dグラフィックスオブジェクトが生成される：
以下の関数は，与えられた多様体の上にNDSolveの解を付加する：
この関数は，さまざまな解の成分をプロットする：

方法の比較

オイラー方程式は，いろいろな積分法を使って解くことができる．そのどれもが異なるコスト，動的特性を持つ．

アダムスの多段階法

ここでは運動方程式を解くのにアダムス法を使う：
以下は，解の軌道を単位球に重ね合せて表示している：
視覚的には，解は球面に閉曲線を描いているように見える．しかし，誤差のプロットによりどちらの制約条件もあまり保持されていないことが分かる：

オイラー法と陰的中点法

まず，指定された固定刻み幅を使ったオイラー法で運動方程式を解く：
これは，指定された固定刻み幅を使った陰的中点法で運動方程式を解く：
以下により，オイラー法を使った運動方程式の数値解を単位球に重ね合わせたもの（左）と，陰的中点法を使った場合のもの（右）を表示する：
これはオイラー法を使った場合の数値解の要素（左）と陰的中点法を使った場合の要素（右）を表示する：

"OrthogonalProjection"法

ここでは"OrthogonalProjection"法を使って方程式を解いてみる：
直交の制約しか守られていないので，曲線は閉じていない：
時間に対する不変量の誤差をプロットすると，正投影法では2つの不変量のうちの1つしか保存されていないことが分かる：

"Projection"法

"Projection"法は制約条件の集団を取り，各積分段階の終りにその解を多様体に投影する．

一般的に問題の不変量すべてを投影に使わなければならない．そうでなければ，数値解は投影されない解よりも実際には質的に劣る可能性がある．

以下は積分法を指定し，NDSolveが呼び出されるまで制約条件の決定を保留する：

1つの制約条件の投影

以下は最初の制約条件を多様体に投影する：
最初の不変量だけが保存される：
第2の制約条件を多様体上に投影する：
2番目の不変量だけが保存される：

複数の制約条件の投影

以下で両方の制約条件を多様体上に投影する：
両方の不変量が保存される：

"Splitting"法

効率的な陽的積分法を作成する分割法は，McLachlan [M93]およびReich [R93]によって別々に導き出された．

常微分方程式 の流れを と書く．

微分方程式系は ，，の3つの要素に分割される．これらはすべてハミルトニアンで，正確に解くことができる．

ハミルトン系が解かれ，各積分段階で以下のように再結合される．

ハミルトニアンのべクトル場への分割を定義する：
これはオイラーの微分方程式系である：
3つに分割されたべクトル場である：

解

これは対称二次分割法を定義する．係数は方程式の構造から自動的に決定され，ストラング(Strang)の分割法の拡張となっている：
系を解き，解をグラフィカルに表示する：
不変量の1つは丸めまで保存されているが，2つ目の不変量の誤差は一定である：