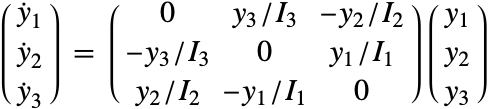刚体求解器

引言方法比较
流形生成和功用函数

引言

一个质心位于原点的自由刚体的运动方程由以下欧拉方程给出（见 [MR99]）.

该系统的两个二次型初积分是：

第一个约束条件实际是把运动从 限制在到一个球面上. 第二个约束表示系统的动能，与第一个不变量一起，把运动限制在球面上的椭圆内.

[HLW02] 中给出了各种方法的数值试验，现在将把各种 NDSolve 方法进行比较.

流形生成和功用函数

加载一些有用的程序包：
定义刚体运动的欧拉方程，以及该系统的不变量：
运动方程沿着单位球上的闭合曲线演化. 这里生成一个三维图形对象来表示单位球体：
这个函数把从 NDSolve 得到的解叠加到给定的流形上：
这个函数画出解的各种分量的图形：

方法比较

可以用各种积分方法来求解欧拉方程，它们各有不同的相关代价和不同的动力学性质.

Adams 多步方法

这里采用一个 Adams 方法来求解运动方程：
这里通过叠加到单位球体上显示了解的轨迹：
该解在看上去给出了球面上的一个闭合曲线. 然而，误差图示表明两个约束被都没有得到特别好的满足：

欧拉和隐式中点法

这里使用具有指定固定步长的欧拉方法求解运动方程：
这里使用具有指定固定步长的隐式中点法求解运动方程：
这里显示用欧拉方法（左）和隐式中点法（右），运动方程的数值解在单位球面上的叠加：
这里显示使用欧拉方法（左）和隐式中点法（右）的数值解的分量：

正交投影法

这里用 "OrthogonalProjection" 方法来求解方程：
只有正交约束是守恒的，所以该曲线不是闭合的：
绘制不变量的误差关于时间的图形，可以看出，正交投影法只保持两个不变量之一不变：

投影法

方法 "Projection" 采用一个约束条件的集合，并且在每个积分步骤的末尾把解投影到一个流形上.

一般来说，问题的所有不变量都应该在投影中使用；否则，数值解可能实际上比未投影的解质量更差.

以下指定了积分方法，并且把约束的确定推迟到 NDSolve 的调用：

投影一个约束

这里把第一个约束投影到流形上：
只有第一个不变量保持守恒：
这里把第二个约束投影到流形上：
只有第二个不变量保持不变：

投影多个约束

这里把两个约束都投影到流形上：
现在两个不变量都保持不变：

"Splitting" 方法

一个产生高效显式积分方法的分裂是分别由 McLachlan [M93] 和 Reich [R93] 独立推导出来.    

把一个常微分方程的流 写为 .

微分系统被分成三个部分：、 和 ，其中每一个都是哈密顿系统，并且可以被精确求解.

哈密尔顿系统被求解，并且在每个积分步重组：

下面定义了哈密顿向量场的一个适当的分裂：
下面是欧拉方程的微分系统：
下面是三个分向量场：

解

这里定义了一个对称二阶分裂法（splitting method）. 其系数自动从方程的结构确定，并且该系数是一个斯特朗分裂（Strang splitting）的扩展：
这里求解该系统，并且用图形显示解：
一个不变量保持在舍入误差内，而第二个不变量中的误差仍然是有界的：