NDSolveの"Composition"法と"Splitting"法

はじめにオプションの要約
例題

はじめに

微分方程式系を部分系に分割し，それぞれを適切な積分法を用いて解くと便利なことがある．それぞれの解を合成することで，体積等の動的特性を保存することができることがある．分割と合成に関する詳細は[MQ02, HLW02]に，NDSolveに関連する特定の問題は[SS05, SS06]に記載されている．

定義

であるときの初期値問題 について考える．

"Composition"

合成は，数値積分法の次数を上げるための便利な手法である．

外挿で使われるエイトケン–ネビル(Aitken–Neville)アルゴリズムとは対照的に，合成ではシンプレクティック法等の基礎的な積分法の幾何的特性を保存することができる．

を，指定された実数 を持ち，刻み幅 を取る基本的積分法とする．

すると， 段階の合成法 は以下のように与えられる．

同じ基本的メソッド を含む合成法 に興味があることがある．

面白い特殊ケースとして，対称合成 （ここで ）がある．

最も一般的な合成には次のようなものがある．

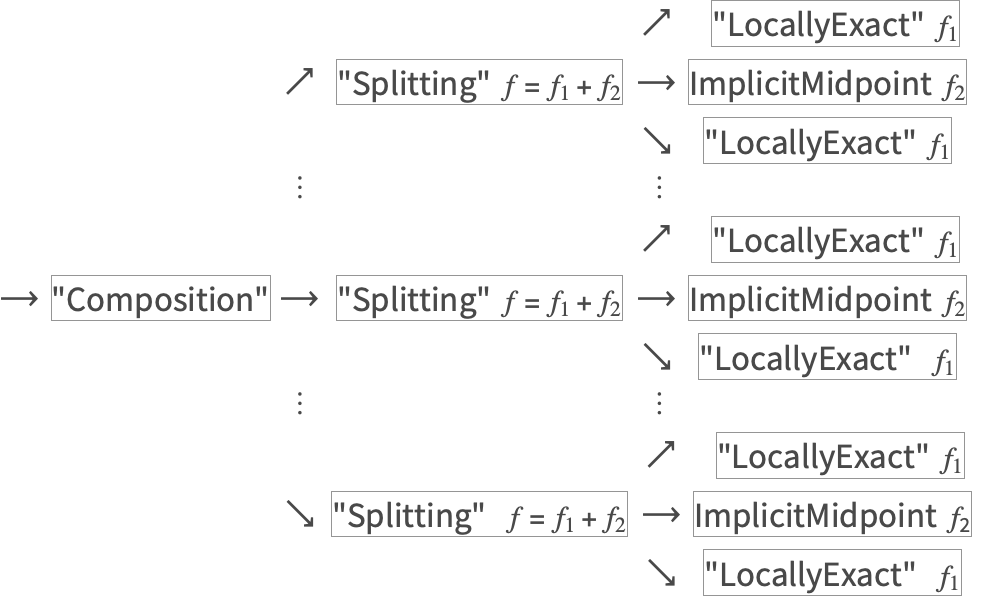
"Splitting"

段階の分割法は，加法的に分割された の合成法の一般化である．

大切なのは， ではなく を含む問題を解く際に，計算上の利点がある場合が多いということである．

段階分割法は，以下の形式の合成である．

ここで は必ずしも異なるものでなくてもよい．

これでそれぞれの基本的積分法が，問題の一部だけを解くようになったが，適切な合成により有利な特性を持つ数値スキームが生まれる可能性がまだある．

べクトル場 が積分可能ならば，厳密解もしくは流れ を数値積分法の代りに使うことができる．

分割法では，流れと数値法を混合して使うこともできる．

その例にLie–Trotterの分割[T59]がある．

を で分割する．すると が一次の積分法を生成する．

計算上では，集団特性を使って流れを合成すると利点が多い．

実装

分割法と合成法を実装するために，新しいNDSolveフレームワークにいくつかの変更を加えることが必要であった．

ネストされたメソッド

以下の例では"Composition"を使って，低次の分割法から高次の分割法を構築する．

NDSolve

簡略化

上記の例で，流れの集合特性を使い，"Splitting"メソッドを直接呼び出すと，より効率的な積分法を得ることができる．

NDSolve

例題

次の例題は，ストラング(Strang)の分割[S68]，[M68]として知られる二次の対称分割を使う．分割係数は，方程式の構造から自動的に決定される．

役に立つ例題を含むパッケージをロードする：
メソッド"SymplecticPartitionedRungeKutta"についてシンプレクティック法のリープフロッグ公式として知られるメソッドを定義する：

シンプレクティック分割

シンプレクティックリープフロッグ

"SymplecticPartitionedRungeKutta"は長期力学を使った，分離可能なハミルトン系 を解くための効率的なメソッドである．

"Splitting"の方が汎用のメソッドであるが，分割されたシンプレクティック法を構築するために使うことができる（しかし，"SymplecticPartitionedRungeKutta"よりもやや効率性に劣る）．

分離可能なハミルトン系 によって支配される線形微分方程式系から派生する調和振動を例に取る：
ハミルトンべクトル場を，運動量および位置を支配する独立の成分に分割する．これは，方程式の右辺をゼロに設定することで実行できる：
この重み付き（一次）オイラー積分ステップの合成は，シンプレクティック（二次）リープフロッグ公式に当たる：

"ExplicitEuler"メソッドは1度しか指定できなかった．2回目と3回目は循環的に埋められるからである．

積分ステップの最後の結果である：
シンプレクティックリープフロッグ積分法に対応する組込みの積分法を実行する：
積分ステップの最後の結果は，分割法の結果と同一である：

シンプレクティックリープフロッグの合成

これは，基本的な積分法としてシンプレクティック法のリープフロッグ公式を使い，Ruth–Yoshidaの対称合成[Y90]を使って四次のシンプレクティック積分法を構築する：
積分ステップの最後の結果である：
これはRuth–Yoshidaの四次メソッドの係数を使って組込みのシンプレクティック積分法を実行する：
積分ステップの最後の結果は，合成法の結果と同一である：

複合メソッド

閉形式の解はべクトル場全体に存在しないことがよくあるが，ベクトル場の一部について微分方程式系を解析的に解くことが可能な場合がある．

DSolveで解が見付かる場合は，局所的に解を求めるのに直接数値評価を使うことができる．

この考えはメソッド"LocallyExact"に実装されている．

調和振動テスト例題

以下の例題は，調和振動方程式の分割成分の厳密な流れの解が，各分割成分にオイラー法を適用したものと同じであることを調べる：

数値・記号複合分割法（ABC flow）

三次元流れを体積保存するためのモデルで，広く研究されているABC flow (Arnold，Beltrami，Childress flow)を考えてみる：

体積保存積分法を直接適用すると，一般に対称性は保存しない．陰的中点公式等の対称保存積分法では，体積を保存しない．

右辺の要素をゼロに設定することで系の分割を定義する：

Y2の系はDSolveで厳密に解くことができるので，"LocallyExact"メソッドを使うことができる．

しかし，Y1は解けないので，分割法の目標の属性を得るためには，適切な数値積分法を使う必要がある．

組込みの"ImplicitRungeKutta"メソッドについて陰的中点公式を計算するメソッドを定義する：
二次の体積保存・反転対称群積分法を定義する[MQ02]：

ロトカ・ヴォルテラ(Lotka–Volterra)方程式

この系のさまざまな数値積分法が「ロトカ・ヴォルテラ方程式の数値解法」の中で比較してある．

オイラー方程式

オイラー方程式のさまざまな数値積分法が，「剛体ソルバ」の中で比較してある．

非自律系のべクトル場

強制平面非自律微分方程式系のDuffing振動子を考える：
これは系の分割を定義する：
べクトル場の時間成分の分割はあいまいであるため，メソッドはエラーメッセージを発する：
Z[T]==Tとなるような新しいダミー変数Z[T]を導入し，分割された微分方程式系でそれをどのように分配するかを指定することにより，方程式を拡張することができる：
これは，あらゆる有限時間に対して （ここで と はリアプノフ指数）を満足する幾何的分割法を定義する[MQ02]：
解のプロットである：

オプションの要約

"Composition"のデフォルトの係数オプションは，Methodオプションを使って指定するメソッドの特性によって，"SymmetricCompositionCoefficients"と"SymmetricCompositionSymmetricMethodCoefficients"のどちらかを自動的に選ぶことを試みる．

オプション名
デフォルト値
"Coefficients"Automatic合成法で使用する係数を指定する
"DifferenceOrder"Automaticメソッドの局所的な精度の次数を指定する
MethodNone数値積分で使用する基礎メソッドを指定する

"Composition"メソッドのオプション

オプション名
デフォルト値
"Coefficients"{}分割法で使用する係数を指定する
"DifferenceOrder"Automaticメソッドの局所的な精度の次数を指定する
"Equations"{}方程式を分割する方法を指定する
MethodNone数値積分で使用する基礎メソッドを指定する

"Splitting"メソッドのオプション