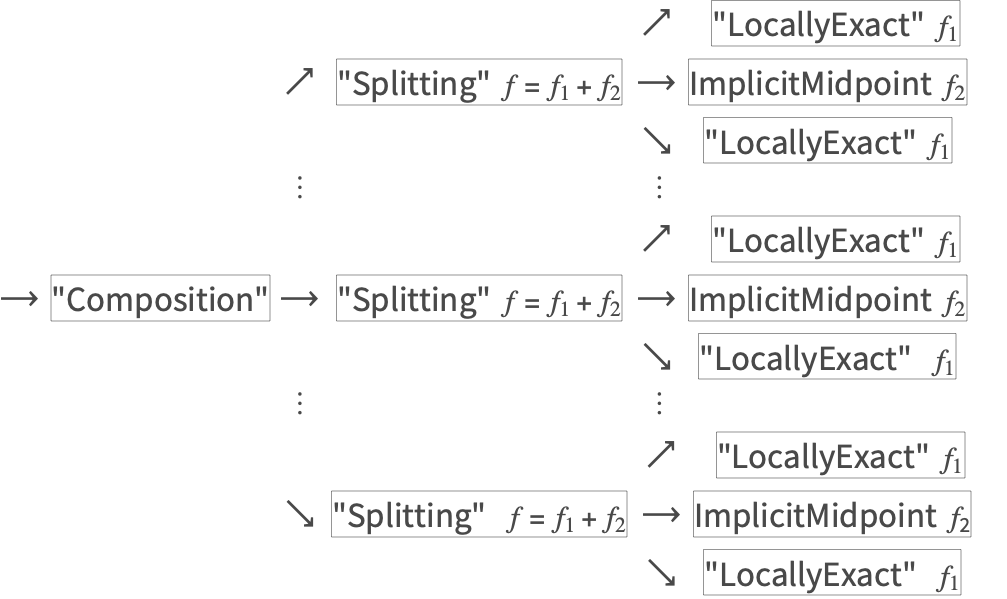
NDSolve 的 “Composition” 和 “Splitting” 方法

引言选项总结
示例

引言

在某些情况下，把微分系统分裂成子系统，并且使用适当的积分方法求解每个子系统是有用的. 重新组合每个单独的解往往允许保留某些动力学属性，比如体积（volume）. 关于分裂和组合的更多信息可以参考 [MQ02, HLW02]，而与 NDSolve 相关的具体方面在 [SS05, SS06] 中进行了讨论.    

定义

我们关注的是初值问题 ，其中 .

"Composition"

组合是提高一个数值积分方案阶数的有用工具.

与在外推法中所用的 Aitken–Neville 算法相反，组合可以保留基本积分方法的几何属性（如辛属性（symplecticity）.

令 为一个基本积分方法，其步长为 ， 是给定的实数.

那么 -级组合方法 由下式给出

通常我们感兴趣的是涉及同样的基本方法 的组合方法 .

一个有趣的特殊情况是对称组合：, .

最普遍的组合类型是：

"Splitting"

一个 -级分裂法是组合方法的一个推广，其中 以加法形式分解：

这里的基本要点是，求解涉及 而不是 的问题往往具有计算优势.

一个 -级分裂法是如下形式的组合

其中 不必不同.

每种基本积分方法现在只求解问题的一部分，但是一个适当的组合仍然可以给出具有优越属性的数值方案.

如果向量场 是可积的，那么精确解或者流 可以用来代替一个数值积分方法.

一个分裂法也可以使用流和数值方法的混合.

一个例子是 Lie–Trotter 分裂 [T59]:

使用 分裂 ；那么 产生一个一阶积分方法.

计算上，利用群的性质把流结合起来更为便利

实现

我们需要对于新的 NDSolve 框架作一些改变，以便执行分裂和组合方法.

嵌套方法

下面例子使用 "Composition" 从一个低阶分裂构建一个高阶分裂法.

NDSolve

简化

在前面的例子中，可以使用流的群属性并且直接调用方法 "Splitting" 来得到一个更加有效的积分器.

NDSolve

示例

下面的例子将使用一个被称为 Strang 分裂的二阶对称分裂 [S68], [M68]. 分裂系数从方程结构中自动确定.

加载一个具有一些有用的示例问题的程序包：
这里以方法 "SymplecticPartitionedRungeKutta" 的形式定义一个被称为辛蛙跳（symplectic leapfrog）的方法：

辛分裂

辛 Leapfrog

"SymplecticPartitionedRungeKutta" 是求解具有良好的长期动力学性质的可分离哈密顿系统 的有效方法.

"Splitting" 是一个更为通用的方法，但是它可以用来构建分区辛方法（虽然效率比 "SymplecticPartitionedRungeKutta" 稍微低一些）.

考虑一个线性微分系统中满足可分的哈密顿 的谐振子.
把哈密顿向量场分裂成与动量和位置相关的独立分量. 这是通过把相关方程的右边设置为零来实现：
加权（一阶）欧拉积分步骤的组合对应于辛（二阶）蛙跳方法：

方法 "ExplicitEuler" 本来也可以只指定一次，因为第二和第三次是以循环的形式填入的.

这是在积分步骤末尾所得的结果：
这里调用对应于辛蛙跳积分器的内置积分方法：
在积分步骤末尾的结果与分裂方法的结果相同：

辛蛙跳的组合

这里采用辛蛙跳方案作为基本积分方法，使用Ruth-Yoshida的对称组合构建四阶辛积分器 [Y90]：
这是在积分步骤末尾所得的结果：
这里使用Ruth和Yoshida的四阶方法的系数调用内置辛积分方法：
积分步骤末尾的结果和合成方法的结果相同：

混合方法

虽然解析解往往在整个向量场上不存在，但在某些情况下有可能解析地对向量场的某部分求解微分方程组.

当使用 DSolve 可以找到一个解时，可以使用直接数值计算来局部推进解.

该思想在方法 "LocallyExact" 中实现.

谐振子测试示例

这个例子检验谐振子方程的分裂分量的精确流的解与对于每个分裂分量应用欧拉方法相同：

混合数值-符号分裂法（ABC 流）

考虑 Arnold、Beltrami 和 Childress 流，这是一个广泛研究的保持体积的三维流的模型：

当直接使用时，一个保持体积的积分器一般将不会保持对称性. 一个保持对称性的积分器，如隐式中点规则，不会保持体积.

这里通过把部分右边的分量设置为零，定义系统的一种分裂：

Y2 的系统通过 DSolve 精确可解，所以用户可以使用 "LocallyExact" 方法.

但是 Y1 不是可解的，因此用户需要使用一个合适的数值积分器来获得分裂方法中所期望的属性.

这里定义了一个方法，用内置 "ImplicitRungeKutta" 方法的形式计算隐式中点规则：
这里定义了一个二阶、保持体积的，倒逆对称群的积分器 [MQ02]：

Lotka–Volterra 方程

这个系统的各种数值积分器在 "求解 Lotka–Volterra 方程的数值方法" 中进行了比较.

欧拉方程

欧拉方程的各种数值积分器在 "刚体求解器" 中作了比较.

非自治向量场

考虑 Duffing 振子，这是一个受迫平面非自治微分系统：
这里定义了系统的一种分裂法：
在向量场中的时间分量的分裂是模糊的，所以该方法发布一个错误提示信息：
该方程可以通过引入一个新的“哑变量” Z[T]，满足 Z[T]==T，并且指明它应该如何在分裂微分系统中分布来扩展：
这里对任意有限时间间隔，定义一个满足 的几何分裂法，其中 和 是Lyapunov 指数 [MQ02]：
以下是解的图形：

选项总结

默认时，"Composition" 中系数选择是根据用 Method 选项指定的方法特性，尝试在 "SymmetricCompositionCoefficients" 和"SymmetricCompositionSymmetricMethodCoefficients" 之间自动选择.

选项名
默认值
"Coefficients"Automatic指定在合成法中使用的系数
"DifferenceOrder"Automatic指定方法的局部准确度的阶数
MethodNone指定在数值积分中使用的基本方法

方法 "Composition" 的选项.

选项名
默认值
"Coefficients"{}指定在分裂法中使用的系数
"DifferenceOrder"Automatic指定方法的局部准确度的阶数
"Equations"{}指定方程应该以哪种方式分裂
MethodNone指定在数值积分中使用的基本方法

方法 "Splitting" 的选项.