置換群
群には多くの異なる表現方法がある.特にすべての有限群は置換群として表現することができる.つまり,有限群は常に位数
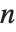
の集合の自己同型の対称群
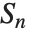
の部分群に同型なのである(ケーリーの定理).この40年の間に置換群の操作で非常に効率的な手法が開発され,大規模な群の操作がコンピュータでできるようになった.
Wolfram言語は,数千の適度な次数の置換群,つまり元の数が

個より多い置換群を扱うことのできるコマンドやアルゴリズムを提供する.
このチュートリアルでは,互いに素な巡回形式で与えられた置換の生成のリストによって指定された有限置換群を使って計算する基本的アルゴリズムをいくつか紹介する.巡回形式の置換の操作方法は,
「置換」で説明する.
群の指定の簡単でコンパクトな方法として,反復される積が群全体を生成するような元の集合を与えるというものがある.これらは群の生成元と呼ばれ,元の集合は生成集合と呼ばれる.これは有限群を指定するためのパワフルで汎用性の高いメソッドであるが,大きい群ではその群についての情報を抽出することが難しい場合もある.
2つの置換を取り,それによって生成される群を構築する:
両方の生成元で点2が固定されているため,この群の中のすべての置換で点2が固定される.これで生成された群は,

通りの置換を持つ集合
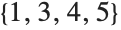
上の対称群と同型な群になる:
小さい群の場合は,群をよりうまく表現することができる.それはケーリーの乗積表とケーリーグラフを使う方法である.ケーリーグラフは群全体と使われている生成集合両方の情報を表す.
小さい群では,ケーリーの乗積表を使ってすべての積を表すことができる:
各行および列は,それ自身が数1
–24の置換である.群がアーベル群であるときかつそのときに限り配列は対称になる.群
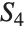
はアーベル群ではない:
ケーリーグラフを使うこともできる.置換
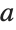
による乗算を赤で,置換
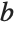
による乗算を青で表す:
グラフを見ると,最初の生成元(赤)は位数3で2番目の生成元(青)は位数2であることが分かる:
グラフの中の閉じたループは,恒等置換となる関係を表す.例えば,ループ
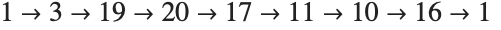
は以下に対応する:
換言すれば,位数4の置換を見付けたということである:
点集合に作用する置換群の生成集合がある場合,指定されたある点に他のどの点が関連し得るかを見付けることができる.これはその点の軌道と呼ばれる.
2つの新たな置換を取り,それを使って生成集合を形成する:
次は点3の軌道である.軌道は点を辞書順に並べ替えて与えられる:
点は2つの異なる軌道に属することはできないため,軌道は群が作用する点集合を分割する.
したがって,軌道は最初の30個の点の範囲を分割する:
軌道は,より多くの点を与えることによって選ぶことができる:
もっと大きい範囲が分割されている場合は,他の点はすべて安定である:
軌道は効率よく計算できるので,大規模な台の置換を扱うことも可能である.
大きい同一位数の2つのランダムな置換により生成された群を取る:
ほとんどの場合,群は単一の軌道で推移的に作用する:
通常,最大長ではないが非常に大きい軌道がまだ存在する:
より一般的な作用を使うと,共役類のような他のタイプの軌道を形成することもできる.
軌道によって与えられる,点がどのように動くかを記述する情報を補完して,1点あるいは複数の点を固定する元の部分群である固定部分群を計算することもできる.
点3を固定する置換の部分群である.巡回表記は,その生成元のいずれも点3を動かさないことを示している:
軌道固定群定理によると,それは群の次数間の商でもある:
置換群が大きいほど,その元をすべてリストしたり描画したりすることが難しくなってくる.そのような場合は,実際にすべての置換を計算しないで,群についての情報が推定できる別の方法を使う必要がある.このもととなる考えは1960年代後半に考案された.それは同じ群に対する同等の新しい生成集合を構築し,その生成集合から群全体が早く操作できる部分群の階層を簡単に作成するというものである.この特殊なタイプの生成集合を強生成集合と呼ぶ.
台
{1,…,24}の2つの置換により生成された次の群を取る:
軌道は標準生成元から直接計算することができる.しかし,群の位数を計算するために,Wolfram言語は内部的にその群に対する強生成元を計算する:
その表現は,もとと同じ生成元の集合に対して再計算するのを避けるために保存される:
生成元の積はどれもこの群に属していなければならない:
ここで強生成集合の属性に戻ろう.強生成元は基底について定義される.基底とは,その群の作用域にある点の順序部分集合であり,その点すべてを固定する唯一の元は単位元である.これは,ある置換のもとの基底にある点の写像を知っていれば,その置換を一意的に見付けることができるということを意味している.基底が短いことが分かっている群は,非常に効率よく操作することができる.基底は,固定部分群の便利な階層を定義する.これは固定群鎖とも呼ばれ,線形代数におけるベクトル空間のガウスの消去法のような階層と同様に,置換群の操作において中心的な役割を果たす.生成元の集合を基底について「強い」と特徴付ける条件は,対応する固定群鎖のすべての部分群に対して,生成部分集合を含んでいるということである.
次は,Wolfram言語によって自動的に選ばれた基底
{1,2,3}についての前出の群の固定群鎖である:
鎖の基底と強生成元は次のように抽出することができる:
鎖の2番目の群は位数253の部分群であり,1の固定群である:
固定部分群の置換は2つ少ない.正確に言うと,点1を動かす置換が欠けているのである:
基底の最初の2つの点に対する固定を繰り返すことができる:
第3の固定群は,基底全体の固定群となっているので,自明な群である:
部分群の大きさは常にもとの群の大きさを割り切るということを示して,ラグランジュ(Lagrange)の定理を確かめる:
オプション
GroupActionBaseによって別の基底を指定することができる.それが真の基底ではない場合,Wolfram言語は追加点を使ってそれを補完する:
最も有名な置換群の一つに,ルービックキューブの回転に関するものがある.次の図では動く面素に1から48までの番号が付いている.中央の面素は動かず,それぞれ6つの基本的な回転を定義する.
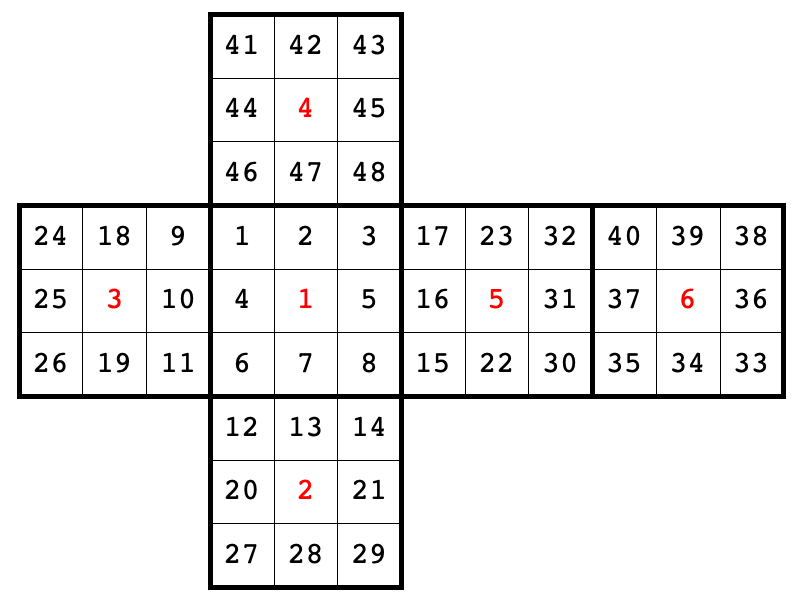
内部的に次の固定群鎖が構築されている.対応する点のリストを固定する置換の数が示されている.1つの置換(恒等置換)だけが指定された18個の点を固定しているので,最終行が群の基底を与える:
次に,いくつかの動きの所属をテストしてみる.例えば辺が隣接した2つの面素は交換できない:
しかしそのような2つの面素を同時に交換することはできる:
次はスーパーフリップと呼ばれ,ここにあるすべてのペアを同時に交換するものである:
次はより台が大きい群の例であるが.どちらも基底は非常に短い.
「ATLAS of Finite Groups」で与えられている最大のシンプレクティック群は,496個の点の置換として表されている

である:
次は819個の点の置換で表される,例外的なねじれ群

である:
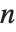 の集合の自己同型の対称群
の集合の自己同型の対称群 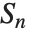 の部分群に同型なのである(ケーリーの定理).この40年の間に置換群の操作で非常に効率的な手法が開発され,大規模な群の操作がコンピュータでできるようになった.
の部分群に同型なのである(ケーリーの定理).この40年の間に置換群の操作で非常に効率的な手法が開発され,大規模な群の操作がコンピュータでできるようになった.