ArcCos[z]
gives the arc cosine ![]() of the complex number
of the complex number ![]() .
.




ArcCos
ArcCos[z]
gives the arc cosine ![]() of the complex number
of the complex number ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- All results are given in radians.
- For real
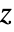 between
between 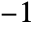 and
and 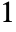 , the results are always in the range
, the results are always in the range 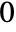 to
to 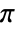 .
. - For certain special arguments, ArcCos automatically evaluates to exact values.
- ArcCos can be evaluated to arbitrary numerical precision.
- ArcCos automatically threads over lists.
- ArcCos[z] has branch cut discontinuities in the complex
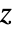 plane running from
plane running from 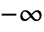 to
to 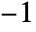 and
and 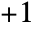 to
to 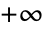 .
. - ArcCos can be used with Interval and CenteredInterval objects. »
Background & Context
- ArcCos is the inverse cosine function. For a real number
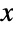 , ArcCos[x] represents the radian angle measure
, ArcCos[x] represents the radian angle measure 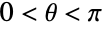 such that
such that 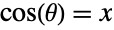 .
. - ArcCos automatically threads over lists. For certain special arguments, ArcCos automatically evaluates to exact values. When given exact numeric expressions as arguments, ArcCos may be evaluated to arbitrary numeric precision. Operations useful for manipulation of symbolic expressions involving ArcCos include FunctionExpand, TrigToExp, TrigExpand, Simplify, and FullSimplify.
- ArcCos is defined for complex argument
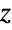 via
via 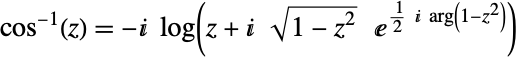 . ArcCos[z] has branch cut discontinuities in the complex
. ArcCos[z] has branch cut discontinuities in the complex  plane.
plane. - Related mathematical functions include Cos, ArcSin, and ArcCosh.
Examples
open all close allBasic Examples (6)
Scope (41)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate ArcCos efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix ArcCos function using MatrixFunction:
Specific Values (4)
Visualization (3)
Function Properties (10)
ArcCos is defined for all real values from the interval ![]() :
:
Complex domain is the whole plane:
ArcCos achieves all real values from the interval ![]() :
:
Function range for arguments from the complex domain:
ArcCos is not an analytic function:
ArcCos is neither non-decreasing nor non-increasing:
It is monotonic over its real domain:
ArcCos is injective:
ArcCos is not surjective:
ArcCos is non-negative over its real domain:
ArcCos has both singularity and discontinuity in (-∞,-1] and [1,∞):
ArcCos is neither convex nor concave:
TraditionalForm formatting:
Integration (3)
Series Expansions (4)
Function Identities and Simplifications (3)
Function Representations (5)
Represent using ArcSec:
Representation through inverse Jacobi functions:
Represent using Hypergeometric2F1:
Representation in terms of MeijerG:
ArcCos can be represented as a DifferentialRoot:
Applications (5)
Properties & Relations (9)
Compose with the inverse function:
Use PowerExpand to disregard multivaluedness of the ArcCos:
Alternatively, evaluate under additional assumptions:
Use TrigToExp to express ArcCos through logarithms and square roots:
This shows the branch cuts of the ArcCos function:
ArcCos gives the angle in radians, while ArcCosDegrees gives the same angle in degrees:
Expand assuming real variables:
Solve an inverse trigonometric equation:
ArcCos is automatically returned as a special case for various mathematical functions:
Possible Issues (4)
Neat Examples (2)
See Also
Cos ArcSin ArcCosDegrees ArcCosh Degree VectorAngle TrigToExp TrigExpand
Function Repository: ArcCosDegree
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1988), ArcCos, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcCos.html (updated 2021).
CMS
Wolfram Language. 1988. "ArcCos." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArcCos.html.
APA
Wolfram Language. (1988). ArcCos. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcCos.html
BibTeX
@misc{reference.wolfram_2025_arccos, author="Wolfram Research", title="{ArcCos}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ArcCos.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arccos, organization={Wolfram Research}, title={ArcCos}, year={2021}, url={https://reference.wolfram.com/language/ref/ArcCos.html}, note=[Accessed: 24-February-2026]}