数学関数
Wolfram言語には膨大な種類の組込み関数が備わっている.
「数学関数」にすべての数学関数の一覧表を示す.ここでは,よく使われるものを紹介する.
| Sqrt[x] | 平方根 (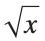 ) ) |
| Exp[x] | 指数関数 ( ) ) |
| Log[x] | 自然対数関数 ( ) ) |
| Log[b,x] |
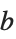 を底とする対数関数 (
を底とする対数関数 (
 )
)
|
| Sin[x]
,
Cos[x]
,
Tan[x] | 三角関数(引数はラジアン) |
| ArcSin[x]
,
ArcCos[x]
,
ArcTan[x] | 逆三角関数 |
| n! | 階乗(整数 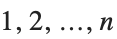 の積) |
| Abs[x] | 絶対値 |
| Round[x] | 小数点1位の四捨五入(  に最も近い整数) |
| Mod[n,m] | |
| RandomReal[] | 乱数(0から1の範囲の擬似乱数) |
| Max[x,y,…]
,
Min[x,y,…] | 集合  , , 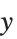 , … , …の最大値,最小値 |
| FactorInteger[n] | |
■ すべての関数の引数は角カッコでくくる. |
■ すべての組込み関数名の先頭文字は大文字で始まる. |
Wolfram言語では関数の引数は角カッコでくくることになっている.丸カッコではいけない.丸カッコは,式の項をまとめるときだけに使う.
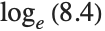
を求める.
Logの関数名が大文字で始まっていることと,引数が角カッコでくくられていることに注意:
引数が厳密値なら,求められる関数の値も厳密である.
平方根

の厳密値を返す:
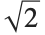
の近似値を返す:
この例では近似を要求していないので,結果は根号の付いた厳密な値で返される:
階乗
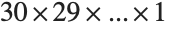
の厳密値を計算させる.階乗の計算ではよく大きな値が得られる.少なくとも
2000!までは,あまり時間をかけずに計算できるはずである:
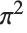
の近似を与える:

の厳密値を求める.三角関数の引数はラジアンであることに注意:

の近似値を求める.定数
Degreeを掛けることで引数をラジアンに変換する:
Log[x]を使って基底
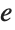
の対数を計算する:
Log[b,x]を使うと,任意の底
b について対数を計算することができる.数学表記法と同様に,
b はオプショナルである: