WXF Format Description
WXF Format Description
WXF is a binary format for faithfully serializing Wolfram Language expressions in a form suitable for outside storage or interchange with other programs. WXF can readily be interpreted using low-level native types available in many programming languages, making it suitable as a format for reading and writing Wolfram Language expressions in other programming languages.
The basic functions for converting between a Wolfram Language expression and its serialized form are BinarySerialize and BinaryDeserialize. Support for reading and writing files with WXF data is built into Export and Import.
| BinarySerialize[expr] | gives a binary representation of any expression expr in the WXF format |
| BinaryDeserialize[bytearray] | recovers an expression from a binary representation in the WXF format |
| Import[file,"WXF"] | imports a WXF file and returns an expression |
| Export[file,expr,"WXF"] | serializes an arbitrary expression and saves it as a WXF file |
| ImportByteArray[ba,"WXF"] | imports data and returns an expression |
| ExportByteArray[expr,"WXF"] |
There are many ways to serialize and deserialize WXF in the Wolfram Language.
Basic Structure
Data in WXF form always contains a plain ASCII header followed by a string of bytes. The header specifies how the bytes can be decoded and is separated by a colon from the string of bytes that represents a sequence of parts.
The byte array continues by giving a sequence of parts, each starting with a token from the following list that specifies the type of the part.
byte value |
character representation (ISO8859-1)
| type of part |
| 102 | "f" | function |
| 67 | "C" | signed 8-bit integer |
| 106 | "j" | signed 16-bit integer |
| 105 | "i" | signed 32-bit integer |
| 76 | "L" | signed 64-bit integer |
| 114 | "r" | IEEE double-precision real |
| 83 | "S" | string |
| 66 | "B" | binary string |
| 115 | "s" | symbol |
| 73 | "I" | big integer |
| 82 | "R" | big real |
| 193 | "Á" | packed array |
| 194 | "Â" | numeric array |
| 65 | "A" | association |
| 58 | ":" | delayed rule in association |
| 45 | "-" | rule in association |
After the token comes, if necessary, a length specification, followed by the sequence of actual content elements for the part.
Basic Examples
Give the bytes for the serialized form of Range[10]:
Examples with Multiple Parts
The examples in the previous section essentially consisted of a single part. There was a single token from the token list, followed by size information, followed by the data. The examples in this section contain multiple parts and types. The first example is shown by the following interactive illustration:
The second example is a list of three elements. The list is represented as a function of length 3, with head List followed by three parts. The first parts introduce the format used to represent integers in a compact form using a token and an "Integer8". The last part shows the representation of a ByteArray:
Give the bytes for the serialized form of {1,-1,ByteArray[{1,2,3}]}:
The head is a symbol of four bytes, namely List:
More on the Header
The header is a plain ASCII string of variable length, delimited by the character ":". For the current version (1.0) of WXF, the first byte in the header is the character "8" (i.e. byte value 56). When the binary serialization is zip compressed, this is indicated in the header by the character "C". The header is never compressed; the compression only applies to the following string of bytes.
Length Encoding (Varint)
WXF types fall into three categories:
- Types with a variable number of subparts like general expressions (token type "f" for function) or Association.
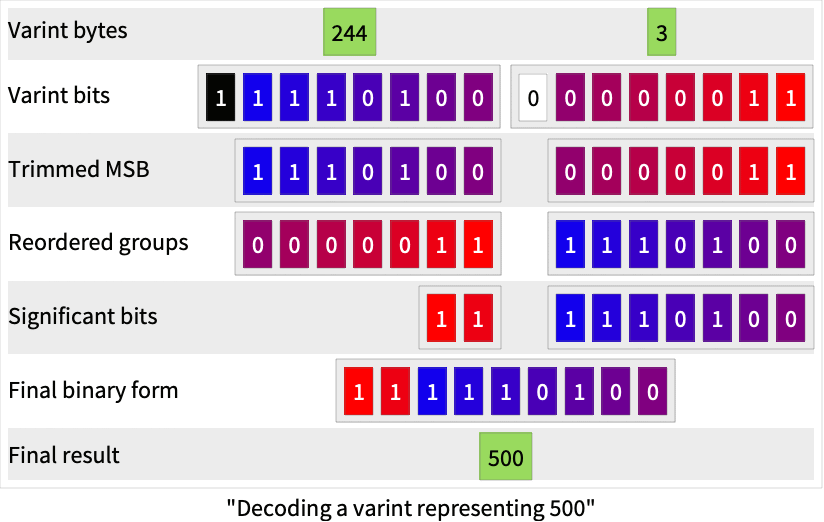
In WXF, all integers representing a length or a size are serialized using the varint method. A varint is a self-indicating variable-length format, where smaller integers require fewer bytes. Each byte except the last one has its most significant bit (MSB) set. The MSB indicates if the following byte of the stream is also part of the varint, acting as a continuation marker. The lower seven bits of each byte store the binary representation of the integer, with the least significant group first.
Order bits of each group, with the most significant bit first, and pad each group so that they have 8 bits each:
The reverse operation of decoding the varint encoded byte sequence {244,3} back to 500 is explained in the following illustration, in which each initial varint bit is assigned a unique color:
Strings, Symbols and Non-Machine Numbers
Strings, symbols and non-machine numbers are represented using the same format. The first byte is a token, then the byte count encoded in the varint format, followed by a string of Unicode characters encoded as UTF-8 corresponding to the string InputForm of the expression. A non-machine number can be either an arbitrary-precision real or an integer that requires more than $SystemWordLength bits to represent.
type of atom | token | representation |
| String | "S" | the Unicode character sequence |
| Symbol | "s" | the fully qualified name of the symbol, specifying the context, except for System` symbols |
| Arbitrary-precision reals | "R" | the digit representation specifying the mantissa and eventually the precision and the exponent |
| Big integers | "I" | the string of digits |
Types based on InputForm.
The next two bytes are 500 in the varint encoding as seen in the preceding example:
Machine Integers Serialization
Machine integers are identified by the smallest integer type from the following list that can represent the value, followed by the two's complement representation of the integer. The byte ordering is always little endian.
token | definition | type size |
| "C" | signed 8-bit integer | |
| "j" | signed 16-bit integer | |
| "i" | signed 32-bit integer | |
| "L" | signed 64-bit integer |
Negative integers binary representation uses the two's complement method. Given a N-bit integer α, its two's complement β is its complement with respect to 2N: α+β=2N. Negation of a number is performed by taking the two's complement.
Machine Reals Serialization
Machine reals are represented using the character "r" followed by the memory representation of a double floating-point value in the IEEE 754 standard. As for machine integers, the byte ordering is always little endian.
Machine-precision complex numbers are serialized as a function of two machine-precision reals. The following illustration highlights the Complex head followed by two real values:
The first bytes after the header are a function of length 2 with head Complex:
The next nine bytes are the real part and match the serialization of the real value 4. as shown in the previous example:
Function Serialization
Functions are represented in WXF by the character "f", followed by the expression length in the varint format. The number of elements is equal to the length incremented by one, for the head. The head and the parts are arbitrary serialized expressions. In particular, the head can also be a function: Select[OddQ][{1,2,3}] is a function of length 1 with head Select[OddQ], which itself is a function with head Select and length 1.
Serialize an expression, using Unevaluated to prevent it from evaluating:
Associations Serialization
An association's rules are represented by the character "-", and delayed rules by the character ":". It is immediately followed by two arbitrary serialized expressions. The length of the association's rule is always two and thus is omitted. The following illustration shows the serialization of a simple association:
Rules of the previous example were part of an association. Rule and RuleDelayed that are not part of an Association are serialized as functions. The serialized form is less packed, as shown in the next example.
The first element is a function of length 2 with head Rule:
The second element is also a function of length 2, but its head is RuleDelayed:
The serialized length is roughly the size of the string FullForm:
Binary Strings
Binary strings are represented by the token "B". They follow the same pattern as strings, but the byte sequence is arbitrary rather than UTF-8 characters. A ByteArray is serialized as a binary string.
The first byte after the header is a binary string token, followed by the length of the binary data:
Numeric Arrays
Arrays are multidimensional tables of machine-precision numeric values. Arrays are represented by the following sequence: a token specifying the type of array, a token specifying the type of the values, the rank in the varint format, the dimensions as a sequence of integers also in the varint format and finally, the data.
There are two types of arrays in the WXF format: packed arrays represented by the token "Á" (byte value 193) and numeric arrays represented by the token "Â" (byte value 194). There are slight differences between the two, the major one being the supported value type, as described in the following tables.
integer value | value in hexadecimal representation | type of array |
| 0 | 0016 | array of 8-bit signed integers |
| 1 | 0116 | array of 16-bit signed integers |
| 2 | 0216 | array of 32-bit signed integers |
| 3 | 0316 |
array of 64-bit signed integers (64-bit system only)
|
| 34 | 2216 |
array of IEEE single-precision real numbers (float)
|
| 35 | 2316 |
array of IEEE double-precision real numbers (double)
|
| 51 | 3316 | array of IEEE single-precision complex numbers |
| 52 | 3416 | array of IEEE double-precision complex numbers |
integer value | value in hexadecimal representation | type of array |
| 0 | 0016 | array of 8-bit signed integers |
| 16 | 1016 | array of 8-bit unsigned integers |
| 1 | 0116 | array of 16-bit signed integers |
| 17 | 1116 | array of 16-bit unsigned integers |
| 2 | 0216 | array of 32-bit signed integers |
| 18 | 1216 | array of 32-bit unsigned integers |
| 3 | 0316 | array of 64-bit signed integers |
| 19 | 1316 | array of 64-bit unsigned integers |
| 34 | 2216 |
array of IEEE single-precision real numbers (float)
|
| 35 | 2316 |
array of IEEE double-precision real numbers (double)
|
| 50 | 3316 | array of IEEE single-precision complex numbers |
| 51 | 3416 | array of IEEE double-precision complex numbers |
The integer range supported by packed arrays varies with the system word length, $SystemWordLength, from -231 to 231-1 on a 32-bit environment, and from -263 to 263-1 on a 64-bit environment.
It is possible to reconstruct the decimal form of each 16-bit integer. First, group the pair of bytes:
Each pair is a little endian 16-bit long integer whose value is reconstructed using a bit shift operation:
The interactive illustration following shows the serialization of the previous matrix before packing. The sequence of elements is significantly different, since it involves nested functions with head List. The inner lists have three parts corresponding to the integer values. It is worth noting that the binary representation of the integer values is similar to the one witnessed in the packed array case (little endian signed 16-bit integer).
Array value type tokens are constructed as bit fields. The four least significant bits store the log of the size of the numeric type in bytes, and the four most significant bits represent the numeric type. Note that for complex types, the size refers to the whole number, so that, for example, the single-precision complex type is considered to have a size of 8 bytes.
It is possible to construct the bit field corresponding to an array of double-precision reals using the Wolfram Language.