EquationTrekkerパッケージ
このパッケージは，微分方程式の他，軌道や軌跡とみなせる解を持つタイプの方程式の解を調べるためのインタラクティブなツールを提供する．
Wolfram言語は，微分方程式の数値解を見付けるために，NDSolveという汎用ツールを提供している．微分方程式を数学形式で簡単に指定できるため，FortranやC++ソルバのパッケージよりも格段に便利になっている．低次元の系では，グラフィカルユーザインターフェースを使って，よりインタラクティブに操作できる．EquationTrekkerを使うと，パラメータの有無を選んで方程式を与えることができ，開いたウィンドウでマウスを使うだけで初期条件を指定することができる．
基本的な使用方法
| EquationTrekker[eqns,y,{x,xmin,xmax},opts] | |
| 範囲が xmin から xmax の独立変数 x を持つ関数 y に対する常微分方程式 eqns の初期条件を指定し，その数値解を表示するためのグラフィカルインターフェースを開く | |
グラフィカルインターフェースを使った，微分方程式の初期条件の選択
EquationTrekkerがどのように動作するかを例示するのに，非常に簡単な例から始めてみる．まず，以下のように入力する．
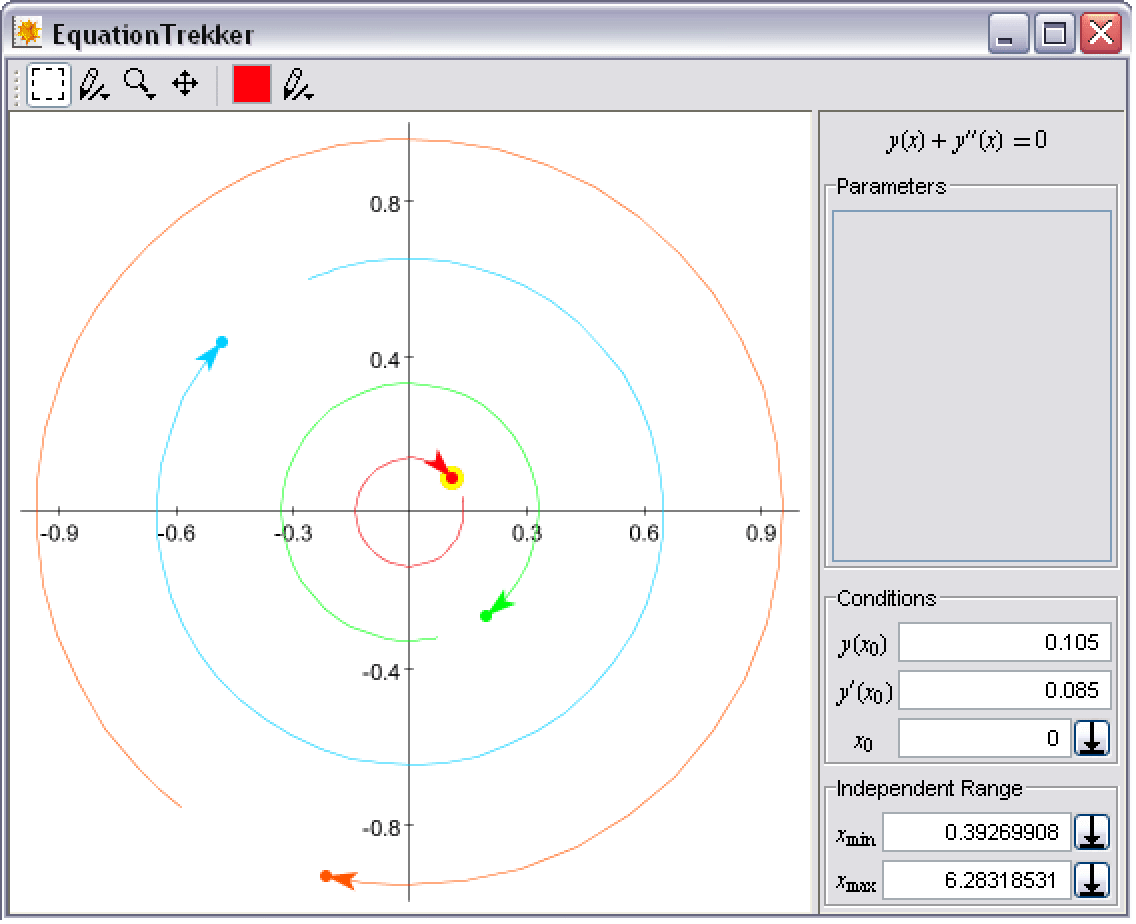
すると，下のような新しいウィンドウが現れる（最初は空白である）．
表示された曲線は「トレック」と呼ばれ，初期条件
からドットで示された点までの解（
，
の位相面で表示）である．デフォルトでは 
はゼロで，トレックはコマンドで与えられた範囲(xmin, xmax)で示される（この例では 
から 
）．初期条件を選ぶためには，カーソルを動かして右クリックするだけでよい．トレックはNDSolveで計算できる状態になるとすぐに表示される（ここの例では，ほんの一瞬である）．マウスの右ボタンを押したままカーソルをドラッグすると，ドラッグに応じて解がリアルタイムで更新される．現在選ばれているトレックは，大きい黄色い円で示される．上のスクリーンショットから分かるように，設定可能な制御や値がたくさんある．その各々については，Wolfram言語インターフェースを示してから説明する．
返されたリストにはEquationTrekkerStateオブジェクトとグラフィックスの2つの要素だけが含まれている．グラフィックスは，ウィンドウが開いている間に生成されたトレックを表示する．EquationTrekkerStateオブジェクトには，ウィンドウが閉じられたときと同じトレックを持つウィンドウを再び開くのに必要な情報がすべて含まれているので，面白い現象を後で調査するために保存しておくことができる．この出力形式は簡略化されており，方程式，変数，初期条件のみを表示する生成されたトレックのリストを示す．
| EquationTrekkerState[eqns,y,{x,xmin,xmax},treks,<data>] | |
| 生成されたトレックを表すリスト treks を使ってEquationTrekkerウィンドウを開くために再利用することのできるデータオブジェクト．データはデフォルトでは出力形で表示されない | |
| Trek[condition,<data>] | 1つのトレックを表すデータオブジェクト．出力形では，トレックを生成するために選ばれた condition のみが表示される |
| EquationTrekker[state] | EquationTrekkerStateオブジェクト state に保存されたトレックでEquationTrekkerウィンドウを開く |
EquationTrekker状態オブジェクト
上のような結果を得るためには，一旦ウィンドウが開かれたときに，Delキーを押して，選んだトレックを削除する．それでウィンドウが閉じられると新しい状態が生成される．
条件は二次元で選ぶ必要があるため，EquationTrekkerは1つか2つの一階方程式，または1つの二階方程式に限られる．2つの一階方程式では上の例とかなり類似したものになる．実は，二階方程式は一階方程式に変換されるのである．やや異なる点は，1つの一階方程式では，点をクリックすると独立変数の初期値を選ぶことになるなるが，2つの方程式では，独立変数の値はゼロであると想定される（これはグラフィカルインターフェースで変更することが可能である）という点である．
パラメータ
複数の初期条件を指定できるということは非常に便利であるが，EquationTrekkerは微分方程式の解の研究を可能にするという点で，その一歩先を行っている．TrekParametersオプションを使うと，記号パラメータを持つ方程式を与えることができ，このパラメータはEquationTrekkerウィンドウインターフェースで制御できる．
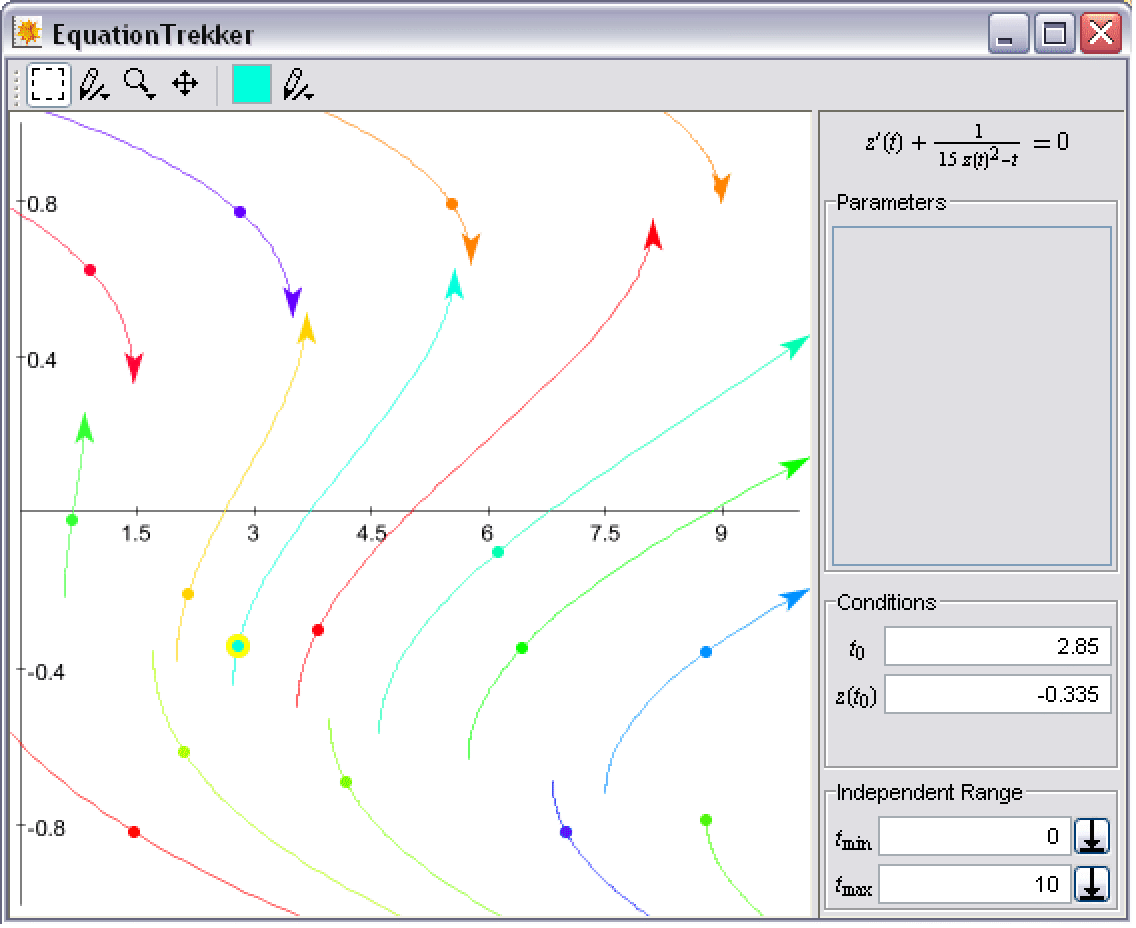
非線形項を含ませると，単純な調和振動よりも面白い方程式になる．
スライダーを動かす（または，テキスト値を変更してEnterを押す）と，新しい解が即座に計算されてウィンドウが更新される．これにより，パラメータがどのように方程式の解に影響を及ぼしたかが一目瞭然である．
パラメータを指定する際に，初期値の他にも取り得る値の範囲を指定することができる．
| name->value | パラメータ name が値 value から始まり，範囲[0,2 value]（value が0のときは[-1,1]）を持つ |
| name->{value,{vmin,vmax}} | パラメータ name が値 value から始まり，範囲[vmin,vmax]を持つ |
インタラクティブな操作ができなければ，このような特性を見つけることはかなり難しかっただろう．
この例を実行して，上記のようにかなりの数のトレックを生成すると，パラメータを変更したときにウィンドウが更新されるのに時間がかかる場合がある．これは，NDSolveがそれぞれの解を再計算しなければならないため，また，急速に変化する非線形項がより解きにくい数値問題を導くため，仕方のないことである．
ポアンカレ(Poincaré)断面
EquationTrekkerのデフォルト動作は，独立変数によってパラメータ化された解の単純なプロットを表示するというものである．しかし，そのようなプロットが非常に混乱を招く場合がある．特に非自律（独立変数に明示的に依存）の方程式等に起りやすい．
このよい例として，駆動型の固定ばりの振動の非線形モデルであるダッフィング(Duffing)方程式が挙げられる．
軌道が互いに横断しており，近隣の点で予想されることが分かりにくい．
全体的な変更を視覚化する方法でよく使われるものに，進行中の関数の一定区間で，解がどのように発展しているかを見るというものがある．これを考えるひとつの方法として，s=Mod[ω t,2π]である三次元空間(x, x′, s)を考えてみるということがある．この場合，解はトーラスの中にある．解の全体的な発展を視覚化するひとつの方法として，解が s 軸に巻きつくたびに，どのように変化するかを見るということがある．つまり，トーラスの1つの断面だけを見るのである．これはポアンカレ断面として知られる，一般的な手法の使い方である．抽出された写像は，ポアンカレ写像と呼ばれる．
上の画像はダッフィング方程式のいわゆるストレンジアトラクタを示している．ストレンジアトラクタは，初期パラメータ値に対する決定論的なカオスを示すものである．軌道を引き付ける性質は，両方の初期条件からの点が最後には同じ構造になるということから直観できる．t の最小値での点が表示されているが，この最小値は過渡電流が減衰するよう，かなり大きいものが選ばれた．このように系を研究するときには，よい選択であるといえる．
ポアンカレ断面のトレックジェネレータを使うためには，メソッドオプションを使って，見たい断面の特性を定義する必要がある．
オプション名
|
デフォルト値
| |
| "SectionCondition" | None | 式がゼロになるとき常に断面変数が示される，問題の変数の式 |
| "SectionVariables" | None | 断面条件式がゼロになるとき常に示される2つの従属変数（二階以上の方程式では変数の導関数でもよい） |
| "FilterFunction" | None | プロットの前に断面変数の値に適用する関数．これはプロットにのみ影響するもので，初期条件の選択範囲には影響しない |
PoincareSectionトレックジェネレータのメソッドオプション
"SectionCondition"と"SectionVariables"の両方に，何らかの値を指定する必要がある．また，計算で使いたいNDSolveのオプションをジェネレータに渡すこともできる．
"SectionCondition"の値がMod[ω t,T]（ここで ω とT は定数で，トレックパラメータに依存することができるが，独立変数 t や任意の従属変数には依存できない）という形式であるとき，この一般的な場合を上記の例のように扱うために，特殊な最適化コードが使われる．
トレックジェネレータの定義
EquationTrekkerは，TrekGeneratorオプションの設定として使えるようになるユーザ自身のトレックジェネレータを，比較的少ない努力で定義できるように設計されている．EquationTrekkerが起動するときに初期化され，独自の引数構造で定義されたメソッドを持つことが想定されているトレックジェネレータオブジェクトの構築を通すことにより，インターフェースが動作する．
| InitializeGenerator[gname,spec,dvars,{ivar,ivmin,ivmax},opts] | gname という名前のトレックジェネレータを，問題指定 spec，従属変数 dvars ，デフォルト範囲が[ivmin,ivmax]である独立変数 ivar，オプション opts で初期化する |
| InitializeGenerator[gname,spec,vars,opts] | gname という名前のトレックジェネレータを，問題指定 spec，変数 vars，オプション opts で初期化する．この場合は，独立変数がないので，EquationTrekkerの引数はNoneとして与えられる |
InitializeGenerator[gname,…]は gname[args]という形式のオブジェクトを返す．オブジェクトの引数 args は，トレックジェネレータが使用するデータを保存するために使うことができる．このデータは，トレックジェネレータ gname の特定の事例に対して特定のものなので，使いやすい形式でよい．gname はSymbolでなければならない点に注意する．
InitializeGeneratorを使って特定のジェネレータを初期化するための規則は，TagSetを使ってジェネレータの名前自体と関連付けておくこと（つまり gname/:InitializeGenerator[gname,…]:=…）をお勧めする．これにより，記号のプロテクトに関する問題や，他のジェネレータの初期化に無意識のうちに影響を及ぼす問題を避けることができる．
トレックジェネレータオブジェクト gobj=gname[args]が定義されると，いくつかのメソッドが定義されるものと想定される．このメカニズムにより，EquationTrekkerは表示形式を決定し，生成された点を取得するのである．
| gobj@"Variables"[] | トレックジェネレータによって使用される変数のリストを返す．独立変数がある場合は，{ivar,dvars}となる |
| gobj@"Display"[] | EquationTrekkerウィンドウの表示エリアに示される方程式あるいは問題を返す |
| gobj@"DisplayMode"[] | トレックのデフォルト表示モード"Line"あるいは"Points"を返す．設定は，EquationTrekkerウィンドウを介して随時変更できるので，これはデフォルトに過ぎない |
| gobj@"FormatTrek"[iv0,X0,{ivmin,ivmax}] | |
| トレックの初期値を指定する独立変数 iv0，従属変数 X0 の値が与えられたときに，トレック指定を説明形式で返す．独立変数が使われていなくても，このメソッドが呼び出されるときには引数が存在するという点に注意する | |
| gobj@"ChangeParameters"[prules] | 規則のリスト prules で与えられる変更されたパラメータ値を使って，迅速に点を生成するのに必要とされる新しいデータを含む新しいトレックジェネレータオブジェクトを返す |
| gobj@"GenerateTrek"[X0,{iv0,ivmin,ivmax}] | |
| 独立変数値 iv0で点 X0=(x0,y0)から始めたトレックに対して生成されたトレック点を返す．点は独立変数の範囲[[ivmin,ivmax]]上に生成される．独立変数がない場合でも，この引数は存在するが値は無視できる．点は座標のリスト{{x1,y1},{x2,y2},…}で与えられる．点を生成する過程で gobj の引数が変更されたら，このメソッドは新しいトレックジェネレータオブジェクトを含むリスト{{points,newgobj}}を返す | |
EquationTrekkerに，変更できる項目や問題の指定を適切な方法で表示させるためには，上記のメソッドがすべて必要である．しかし特定のトレックジェネレータの中核は，"GenerateTrek"メソッドがどのように定義されるかによる．
トレックジェネレータ設定の背後にある考えは，例を見ると分かりやすい．以下に挙げる2つの例は，その目的で簡単にしてある．パッケージファイルEquationTrekker.mでもDifferentialEquationTrekとPoincareSectionジェネレータの定義を見ることができる．
例：Nesting
これは，指定された関数にNestList を適用した結果をプロットするだけの簡単なジェネレータである．基本的な概念は簡単であるが，反復の概念はほとんどの数値法で基本となるものなので，多様なメソッドやモデルがこの方法で可視化できる．
メソッドによって保存されるハミルトニアンの等高線は，上の画像から非常にはっきり分かる．これとは対照的に，通常の前進オイラー法は振子方程式に対して無条件に不安定であるため，外側に向いた螺旋を描く点を表示する．h をゼロ近くに変更すると，等高線は振子方程式の実際の軌道により類似したものになり，安定領域付近の曖昧さがなくなる．
コンテキストに関する注意
EquationTrekkerの構築のもととなった GUIKit アプリケーションは，同時に呼び出されるというコンフリクトを避けるために，コンテキストパス（$ContextPathで与えられる）に明示されていないコンテキストにある入力シンボルのコンテキストを変更する．
Global`コンテキストのシンボルはプライベートコンテキストによって与えられる．通常，新しいシンボル名を入力すると，そのコンテキスト内に生成されるので，コンテキストを考慮せずに作成した定義は，EquationTrekkerを起動したときに認識されない可能性がある．上記のネスト例題でこのような問題を避けるためには，EquationTrekkerパッケージが最初にロードされたときにコンテキストパス上に置かれたEquationTrekker`コンテキストに，Nestingを置くことができる．
整然とした方法で行いたい場合は，トレックジェネレータの定義を含むパッケージ（つまりNesting`）を作るとよい．これでパッケージをロードすると，そのコンテキストがコンテキストパスに置かれるので，定義が適切に動作する．この方法は，次の例で示す．
例：FindMinimum
独立変数を使用しない簡単な例には，FindMinimumを使って，選ばれた初期値から始めて到達された探索点を示すだけのトレックジェネレータがある．
このジェネレータと前の例題のジェネレータとの最も大きな違いは，このジェネレータでは独立変数を使わないという点である．これは独立変数を持つ引数が単に省略されるということでInitializeGeneratorに反映される．使用された変数だけが返される"Variables"メソッドの他に，他のメソッドの引数が同じ構造を持つ．たとえ独立変数が使われなくても，いくつかの（意味のない）値が渡されるのである．これは，EquationTrekkerの全体的な操作を最適化するために起る．
前の定義でもう1点言及したいのは，オプションが渡される方法である．FindMinimumオプションはFilterRulesで選ばれ，トレックが生成される度に保存される．これらのオプションは，EquationTrekkerが起動されたときにこれに与えられたオプションから来ている．
インタラクティブな制御
EquationTrekkerのグラフィカルインターフェース制御は，概して自己説明的である．以下に，制御の参照をその簡潔な使用法説明とともに列挙する．
EquationTrekkerウィンドウの上部に，トレックツールバーが表示される．
最初の4つの制御では，現行モードを変更することができる．最後の2つでは，色の選択および現行の描画モードの表示ができる．
アイコン
|
モード
| |
| トレック選択モード | マウスボタンでトレックを選ぶ．ドラッグまたはShift+クリックを使うと，複数トレックが選択できる．一旦トレックが選択されると，以下のことが可能である
• Delキーを使ってトレックを削除する
• ドラッグして初期位置を動かす
• カラーツール
|
| トレック作成モード | マウスボタンで新規トレックが作成できる Ctrl+クリックあるいは右クリックでトレックを選択する create treksボタンをドラッグすると，デフォルト描画モードで線と点とを切り替えることができる．ツールバーの最後の項目は，現行の描画モードを表す |
| ズームモード | ズームモードでは，以下のことができる． • マウスをドラッグすると，新しい範囲となる四角形が表示される．デフォルトの動作は，現行のグラフの縦横比を維持する四角形を使うことである．ドラッグ中にCtrlキーを押すと，縦横比が変更できる長方形に変わる • Shift+ドラッグで，現行のプロット範囲がマップ（ズームアウト）される四角形が表示される • Ctrl+ドラッグ（右ドラッグ）でパンされる Zoom Modeボタンをドラッグすると，zoom to fitあるいはscale to fitが選べるメニューが開く．zoom to fitは，縦横比を維持したままですべての軌道が収まる領域を見付ける．scale to fitはすべての軌道が収まる最小のプロット範囲を見付ける |
| パンモード | マウスボタンで，選択された点を中心にパンする．ドラッグすると，インタラクティブにパンできる．右クリックあるいはCtrl+クリックでズームされる |
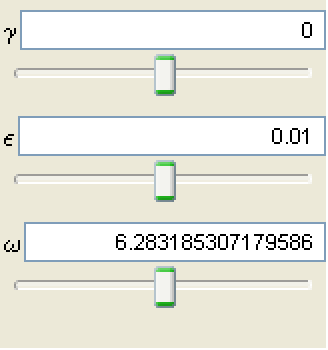
parameterパネルにより，TrekParametersオプションを使って指定したパラメータがどれでも変更できる．
パラメータ値は，スライダーを使ってもテキストフィールドに希望の値を入力してEnterを押しても変更できる．
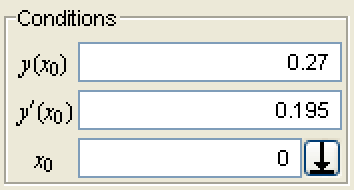
conditionsパネルは通常初期位置，（存在する場合は）独立変数の初期値を反映する．
すべての値は，トレックの位置をグラフィカルに動かしても，希望の位置を入力してEnterキーを押しても変更できる．
独立変数がある場合は，以下のような独立変数の範囲を示すパネルが表示される．
値を入力すると，選択されたトレックの独立変数の値の範囲が変更できる．
